(рис.1)
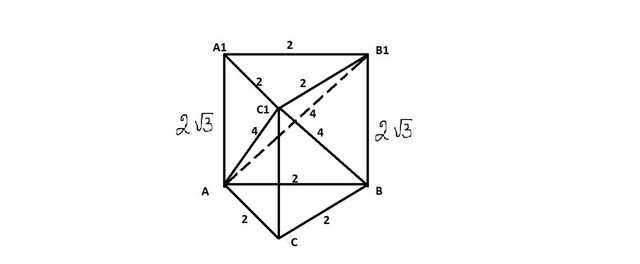
Заметим, что данная призма составлена из 3-х пирамид с вершинами
АА1В1С1; С1АВС и ВАВ1С1
АА1=ВВ1 - перпендикуляры к основаниям АВС и А1В1С1 а значит высоты пирамид АА1В1С1 и С1АВС
Vпризмы=Sabc*h=(a²√3/4)*AA1=(2²√3/4)*2√3=6
Vaa1b1c1=(1/3)*Sa1b1c1*AA1=(1/3)*(2²√3/4)*2√3=2
Vc1abc=(1/3)*Sabc*CC1=(1/3)*(2²√3/4)*2√3=2
Vbab1c1=6-2-2=2
Sab1c1=√p(p-a)(p-b)(p-c)=√5(5-4)(5-4)(5-2)=√15
Vbab1c1=(1/3)*Sab1c1*h
2=(1/3)*√15 *h
h=6/√15
мы нашли высоту (перпендикуляр) опущенную на плоскость АС1В1
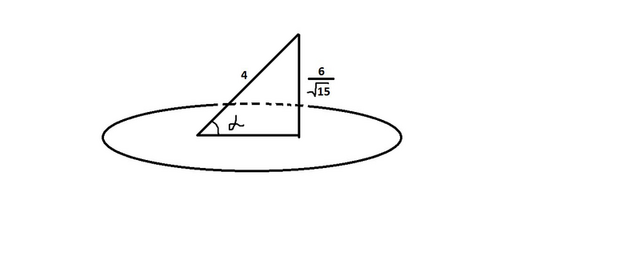
угол между прямой и плоскостью-это угол между самой прямой и проекцией на эту плоскость
если нам известна сама наклонная и перпендикуляр, то можно найти синус нужного угла (рис.2)
sinα=h/BC1=6/4√15=3/2√15=3√15/30=√15/10
α=arcsin√15/10
отв:α=arcsin√15/10