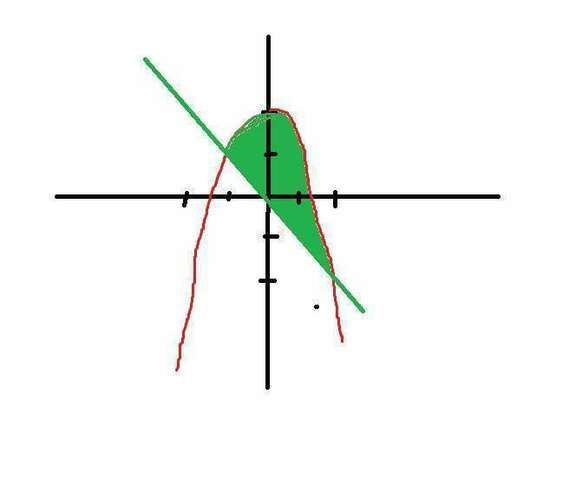
Для начала нужно найти точки пересечения графиков, их абсциссы будут пределами интегрирования.
-х²+2 = -х
х²-х-2 = 0
х=2, х=-1 - пределы интегрирования.
Верхняя граница фигуры - парабола, нижняя - прямая.
S =-₁ ∫²(-x²+2-(-x))dx =( -1/3x³+2x+1/2x²)|-₁ ² = (-1/3*8+2*2+1/2*4) - (-1/3*(-1)+2*(-1) +1/2*1) = -8/3+4+2-1/3+2-1/2 = 4,5