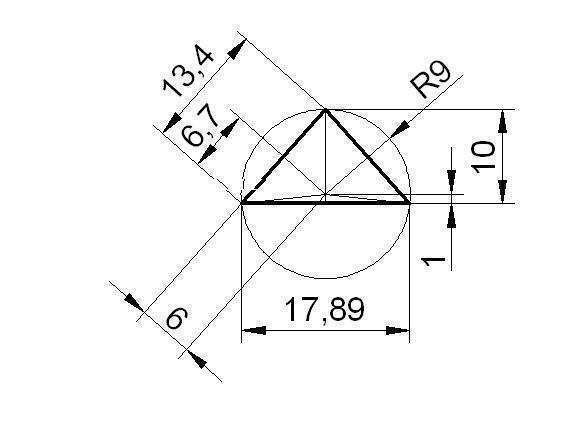
Расстояние от центра окружности до середины основания: c = V(R^2 - ((8V5 / 2)^2) =
=V((9^2 ) - (17,8888 / 2)^2) = V(81 - 80) = 1.
Отсюда высота треугольника h = 1 + 9 = 10.
Боковая сторона равна V((10^2) + (8V5 / 2)^2) = V(100 + 80) = 13,4164.
Искомое расстояние представляет собой катет в треугольнике, гипотенузой которого является радиус, а вторым катетом - половина боковой стороны.
k = V(9^2 - (13,4164 / 2)^2) = V(81 -45) = V 36 = 6.