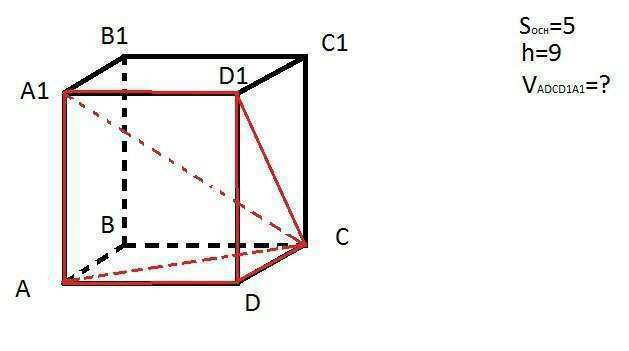
Фигура, объем которой требуется найти, является пирамидой, в основании которой лежит A1D1DA, вершиной пирамиды является точка C. Объем пирамиды равен V=1/3 * S * H, где S - площадь основания, H - высота пирамиды.
Так как CD⊥AD, CD⊥DD1, то CD⊥(AA1D1), то есть плоскости основания пирамиды. Это значит, что H = CD.
Так как призма, в которую вписана пирамида, является правильной, в основании ее лежит правильный четырехугольник, то бишь квадрат. Можно найти сторону квадрата, зная его площадь. AD = √5. Найдем площадь основания пирамиды. Основание пирамиды - прямоугольник, так как, опять же, призма правильная, а значит, прямая. Sосн = A1A * AD = 9√5.
V = 1/3 * Sосн * H = 1/3 * 9√5 * √5 = 15.