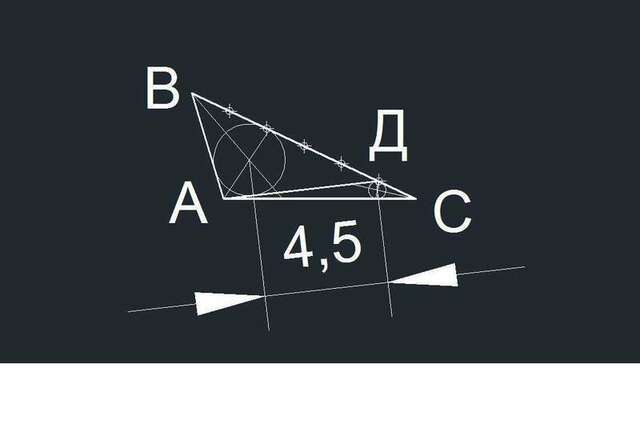
На основе теоремы косинусов:
- по сторонам треугольника АВС находим косинус угла В:
cos B = 949+81-16)/(2*7*9) = 114/126 = 19/21.
- используя это значение, находим длину АД:
АД = √(49+2,25-2*7*1,5*(19/21)) = √32,25.
Зная длины сторон треугольников АСД и АВД по формуле:
r = S/p, где S - площадь, а p - полупериметр, находим радиусы вписанных окружностей в треугольники АСД и АВД.
r(АСД) = 1,3016357.
r(АВД) = 0,3154076.
Находим расстояние между центрами окружностей (используя координаты их центров): О1О2 = 4,78172.
Расстояние L между точками E и F равно:
L =√(O1O2)²-(r1+r2)²) = √(4,78172²-(1,3016357+0,3154076)²) =
= √(
22,8648-
2,61483) = √20,25=
4,5.
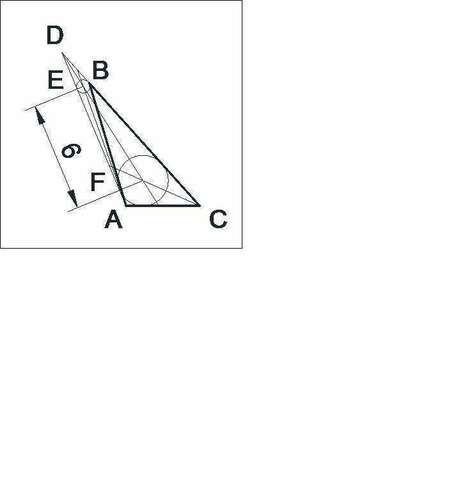
Рассмотрим второй вариант решения, когда точка Д находится на продолжении стороны ВС.
Пусть длина отрезка ВД - это х.
Из заданного соотношения ВД : ДС=1 : 5 находим х/(х+9) = 1/5.
5х = х + 9,
4х = 9,
х = 9/4 = 2,25.
Длина ДС = 2,25 + 9 = 11,25.
Косинус угла С не изменился и равен 2/3.
АД = √(4²+11,25²-2*4*11,25*(2/3)) = √82,5625 ≈
9,0863909.
Расстояние от вершины треугольника до точки касания вписанной окружности находим по формуле: L = p-a, где р - полупериметр треугольника, а - сторона, имеющая общий угол с искомым отрезком.
Находим: р(АДС) = (11,25 +
4 + 9.0863909)/2 =
12.168195.
р(АВС) = (2,25 + 9,0863909 +
7)/2 =
9,168195.
Получаем длину EF = 6.