У такой функции область значений ограничена только тем, что знаменатель не может быть равен нулю. Для нахождения этого условия решим квадратное уравнение:
3х^2 + 2x -1 = 0
D = 4 + 4*3 = 16 = 4^2
x1,2 = ( -2 +- 4 ) / 6 = {-1; 1/3}
То есть в точках х=-1 и х=1/3 функция имеет разрывы.
Далее график в принципе можно построить по точкам с учётом, что это будет гипербола (так как х присутствует только в знаменателе) и скорее всего он будет уходить в бесконечность и менять знак в точках разрывов.
Возьмём точки например:
х=1 тогда y=-1/(3+2-1)=-1/4
x=2 тогда y=-1/(12+4-1)=-1/15
x=3 y=-1/(27+6-1)=-1/32
Значит в правой части - гипербола от минус бесконечности растёт до нуля, и проходит через эти точки
х=-2 у=-1/(12-4-1)=-1/7
х=-3 y=-1/(27-6-1)=-1/20
Значит в левой части гипербола от нуля падает до минус бесконечности
Осталась центральная часть, тут она будет сначала падать от бесконечности и потом возрастать обратно. Наименьшего значения она достигнет посередине интервала. Найдём это точку:
х=-1/3 у=-1/(1/3-2/3-1)=3/4 - это минимум функции на интервале
И на всякий случай найдём пару вспомогательных точек:
х=0 тогда y=1
х=-2/3 y=-1/(4/3-4/3-1)=1
Через эти точки пройдёт график
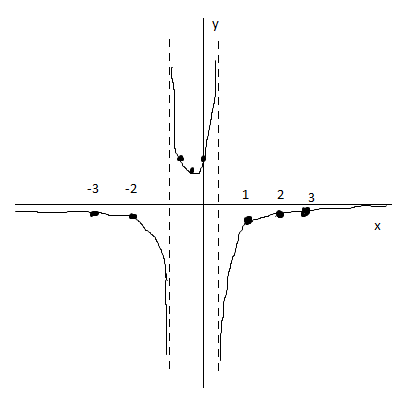
На всякий случай прилагаю ужасающую иллюстрацию из пэинта, если что - спрашивайте