Задание 1. Всего количество чисел от 10 до 60 - 60-9=51. Среди них, количество чисел, делящихся на 4 равно 13 (12;16;20;24;28;32;36;40;44;48;52;56;60)
Искомая вероятность : P=13/51 ≈ 0.25
Задание 2. Выбрать один белый шар можно

способами, а два черных шара -

способами. По правилу произведения, вынуть один белый шар и два черных шара можно 15*10=150 способами (кол-во благоприятных событий)
Количество все возможных событий:
 Искомая вероятность:
Искомая вероятность:  Задание 3.
Задание 3. Выбрать одного мужчину можно 20 способами, а трёх женщин -

способами. И тогда выбрать делегацию из четырёх человек(1 мужчина и 3 женщин) можно 20*120=2400 способами.
Количество все возможных событий:
 Искомая вероятность
Искомая вероятность  Задание 4.
Задание 4. Число испытаний: n=3, вероятность успеха - 0,8, вероятность неудачи - q=1-0.8=0.2. Искомая вероятность по формуле Бернулли:
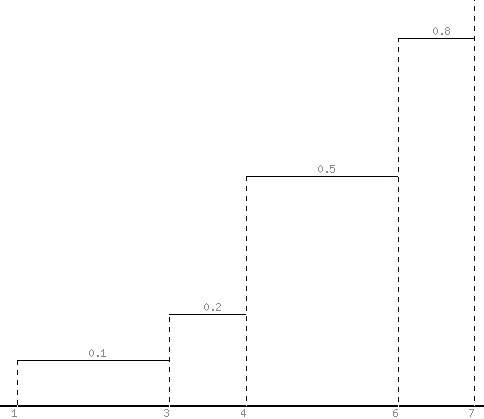
 Задание 5.
Задание 5.  Задание 6.
Задание 6. В таблице вероятности сумма вероятностей должна равняться 1, то есть

Вычислим математическое ожидание по определению


Дисперсия:

Среднее квадратическое отклонение σ(x)
.