НУЖНА ПОМОЩЬ!:) в шар вписан конус, высота и радиус основания которго соответственно...

0 голосов
205 просмотров

НУЖНА ПОМОЩЬ!:)

в шар вписан конус, высота и радиус основания которго соответственно равны 3см и 3корень из3 см. Найти объем шара

Геометрия (196 баллов) | 205 просмотров
Дан 1 ответ
0 голосов
Правильный ответ

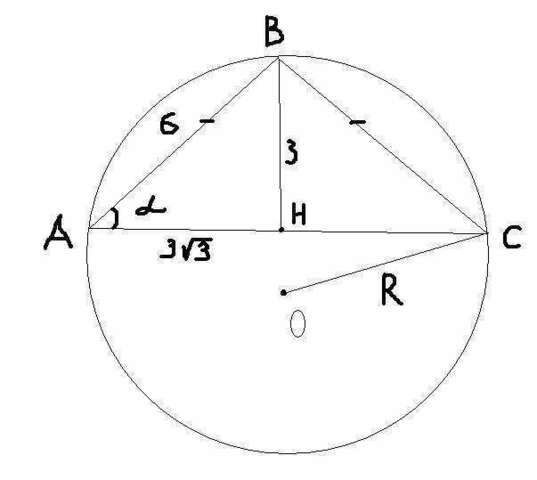
Здесь следует рассмотреть сечение шара плоскостью, которая делит и шар,и конус таким образом, что все мы наблюдаем как бы в срезе. Смотри рисунок. Используем расширенную теорему синусов, чтобы узнать радиус описанной окружности вокруг треугольника АВС. Заметим, что этот треугольник равнобедренный.  АВравно ВС как образующие конуса. Найдем АВ по теореме Пифагора

AB^2=AH^2+HB^2

AB^2=(3\sqrt3)^2+3^2

AB^2=27+9

AB^2=36

AB=6 см.

Найдем противолежащий угол ВСА. Он равен углу ВАС.

 

По теореме синусов нам нужен синус этого угла.

\sin\angle BAC=\frac{BH}{AB}

\sin\angle BAC=\frac{3}{6}

\sin\angle BAC=\frac{1}{2}

 По теореме синусов

2R=\frac{AB}{\sin\angle BCA}

2R=\frac{6}{\sin\angle BAC}

2R=\frac{6}{0,5}

2R=12

 

R=6 - радиус описанной окружности вокруг треугольника АВС, и радиус шара описанного вокруг конуса одновременно.

 

Объем шара находится по стандартной формуле

 

V=\frac{4}{3}\pi*R^3

 

V=\frac{4}{3}\pi*6^3

V=4\pi*6^2*2

V=8\pi*36

V=288\pi

image
(114k баллов)
Похожие задачи