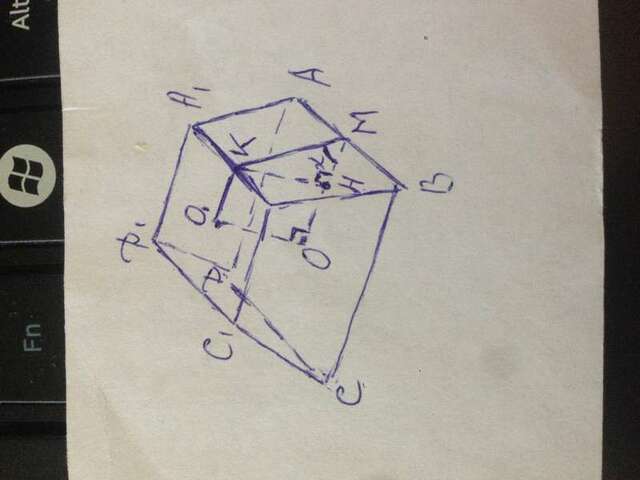
АВСДА1В1С1Д1 - усечённая пирамида. О1О - высота, О1К⊥А1В1, ОМ⊥АВ, КН⊥МО, А1В1=а, АВ=b, ∠КМО=α.
Объём усечённой пирамиды вычисляется по формуле:
V=h(S1+√(S1·S2)+S2)/3, нужно найти h.
В основаниях пирамиды лежат квадраты, значит О1К=А1В1/2=а/2 и ОМ=АВ/2=b/2.
МН=ОМ-ОН=ОМ-О1К=(b-а)/2.
В треугольнике КМН tgα=КН/МН ⇒ КН=МН·tgα=tgα·(b-a)/2.
В пирамиде О1О=КН.
Объём пирамиды равен:
V=tgα·(b-a)(a²+ab+b²)/6=tgα(b³-a³)/6 это ответ.