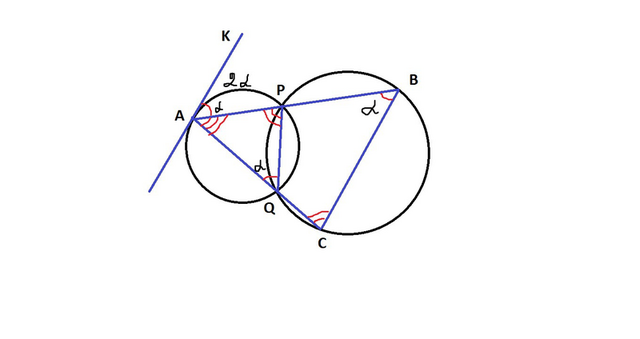
В большую окружность вписан четырехугольник PBCQ
Теорема: " Если в окружность вписан четырехугольник, то сумма его противоположных углов равна 180° ".
то есть, если ∠АВС=α, то ∠CQP=180-α
углы АQP и CQP - смежные, значит их сумма равна 180°
Если ∠CQP=180-α, то ∠АQP=180-(180-α)=180-180+α=α.
Следовательно ∠АВС=∠АQP
2) ∠ АQP - вписанный, опирается на дугу АP
Теорема:"Вписанный угол равен половине дуги, на которую опирается".
То есть, дуга АР= 2∠АQP=2α
3)Теорема: " Угол между касательной и хордой равен половине отсекаемой дуги".
То есть, ∠KAP = дуга АР / 2=2α/2=α.
следовательно AK || BC, так как ∠АВС=∠KAP - накрест лежащие углы - ч.т.д