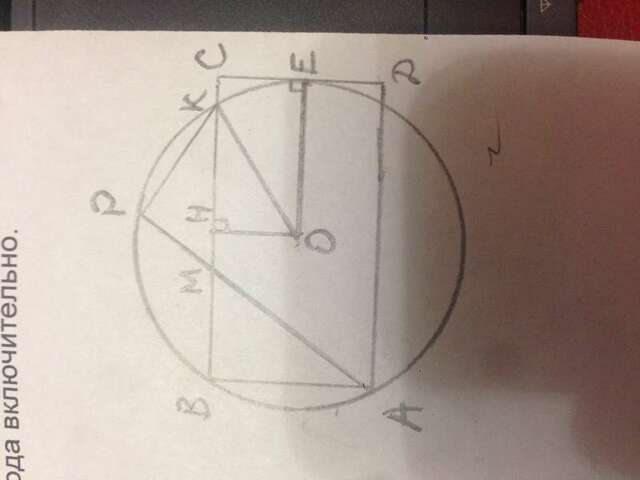
АР и ВК - пересекающиеся хорды.
Благодаря свойству пересекающихся хорд можно записать следующее тождество: АМ·РМ=ВМ·КМ ⇒ ВМ=АМ·РМ/КМ=15·4.2/7=9.
В тр-ке АВМ АВ²=АМ²-ВМ²=15²-9²=144,
АВ=12.
В тр-ке АВК ВК=ВМ+КМ=9+7=16.
АК=√(АВ²+ВК²)=√(12²+16²)=20.
Центр окружности, точка О, делит диагональ АК пополам. ОК=АК/2=10.
Окружность касается стороны СД в точке Е. ОЕ - радиус окружности, ОЕ=ОК=10.
Проведём перпендикуляр ОН к стороне ВК. ВН=ВК/2=16/2=8.
ОК=ОЕ=10.
В прямоугольнике ОНСЕ НС=ОЕ.
ВС=ВН+НС=8+10=18 - это ответ