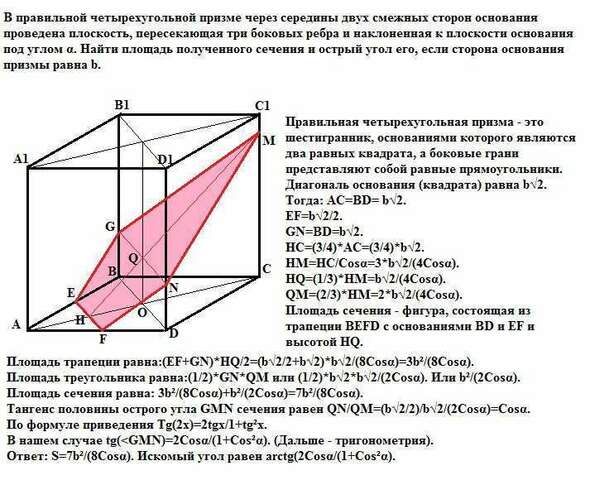
"Правильная четырехугольная призма - это шестигранник, основаниями которого являются два равных квадрата, а боковые грани представляют собой равные прямоугольники".
Диагональ основания (квадрата) равна b√2.
Тогда: АС=ВD= b√2.
ЕF=b√2/2.
GN=BD=b√2.
HC=(3/4)*AC=(3/4)*b√2.
HM=HC/Cosα=3*b√2/(4Cosα).
HQ=(1/3)*HM=b√2/(4Cosα).
QM=(2/3)*HM=b√2/(2Cosα).
Площадь сечения - фигура, состоящая из трапеции GЕFN c основаниями GN и EF и высотой НQ и равнобедренным треугольником GNM c основаниями GN и высотой QM.
Площадь трапеции равна:(EF+GN)*HQ/2=(b√2/2+b√2)*b√2/(8Cosα)=3b²/(8Cosα).
Площадь треугольника равна:(1/2)*GN*QM или (1/2)*b√2*b√2/(2Cosα). Или b²/(2Cosα).
Площадь сечения равна: 3b²/(8Cosα)+b²/(2Cosα)=7b²/(8Cosα).
Тангенс половины острого угла GMN сечения равен QN/QM=(b√2/2)/b√2/(2Cosα)=Cosα.
По формуле приведения Tg(2x)=2tgx/1+tg²x.
В нашем случае tg(Ответ: S=7b²/(8Cosα). Искомый угол равен arctg(2Cosα/(1+Cos²α)).
P.S. (Дальше - тригонометрия для желающих).