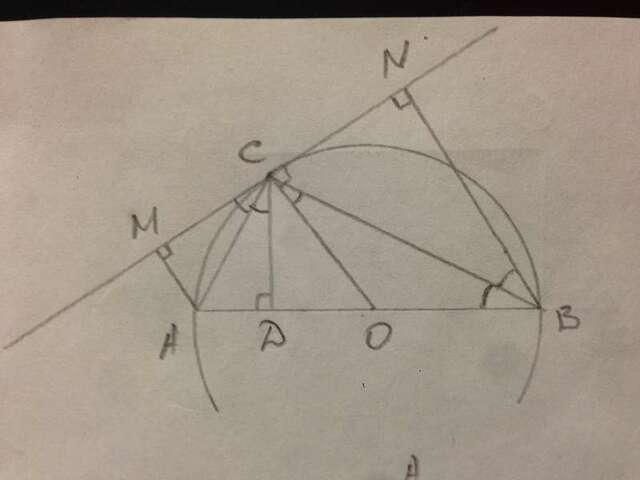
В тр-ке АВС ∠А=α, ∠В=β, ∠С=90°.
АМ⊥MN и BN⊥MN. СО - радиус описанной окружности и одновременно медиана, СО⊥MN. АМ=а, BN=b.
СО=ВО, значит тр-ник ВОС - равнобедренный, ∠ВСО=∠СВО.
Тр-ки АВС и АСД подобны, т.к. ∠А - общий и оба прямоугольные, значит ∠АСД=∠В=β
∠ДСО=∠С-∠АСД-∠ВСО=90°-2β.
∠АМС=∠МСО-∠АСД-∠ДСО=90-β-(90-2β)=β ⇒ ΔАСД=ΔАСМ (по углам и общей стороне), значит АД=АМ=а.
∠ВСN=∠NCO-∠BCО=90-β=α, значит ΔВСN=ΔВСД (по углам и общей стороне), значит ВД=BN=b.
В тр-ке АВС СД - высота СД²=АД·ВД=ab.
В тр-ке АСД АС=√(АД²+СД²)=√(a²+ab)=√[a(a+b)] - это ответ.
В тр-ке ВСД ВС=√(ВД²+СД²)=√(b²+ab)=√b[(a+b)] - это ответ.