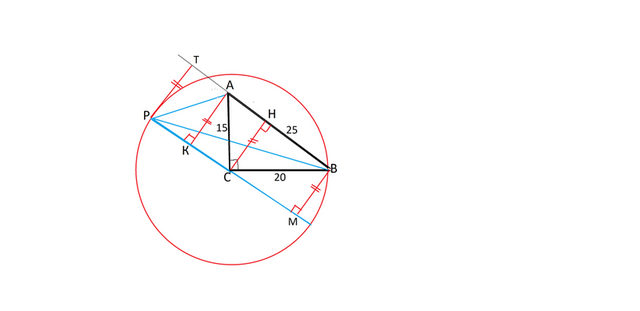
В решении этой задачи больше рассуждений, чем собственно вычислений.
Из условия ясно, что, поскольку
СВ=20=r,
а С - центр окружности,
то вершина В треугольника АВС лежит на окружности,
а А - внутри окружности, т.к. АС меньше радиуса.
Из соотношения сторон треугольника АВС
АС:ВС:АВ=15:20:25=3k:4k:5k (k=5) видно, что треугольник этот - египетский и потому - прямоугольный, с прямым углом С.
Сделаем рисунок.
Для того, чтобы треугольники АРС и ВРС были равновелики, они
при равных основаниях должны иметь равные высоты.
АК=ВМ, РС - общее основание.
Но при АК=ВМ прямые АВ и РМ должны быть параллельны;
получаем четырехугольник с равными параллельными сторонами АК=ВМ, равными углами при стороне РМ. Отсюда АКМВ - прямоугольник.
И АВ||КМ.
Обратим внимание на то, что высота СНтреугольника АВС равна высотам треугольников АРС и ВРС -
все точки одной параллельной прямой находятся на одинаковом расстоянии от другой параллельной прямой.
Следовательно, расстояние РТ от точки Р до прямой АВ равно высоте СН треугольника АВС.
Высоту СН найдем из площади треугольника АВС.
Т.к. треугольник, как мы выяснили, прямоугольный, его площадь равна половине произведения катетов.
S =AC*BC:2=15*20:2=150
Но в то же время площадь равна половине произведения высоты СН на АВ:
S= СН*АВ:2=150
CH=2S:АВ=300:25=12
РТ=СН=12
Ответ: Расстояние от точки Р до прямой АВ=12