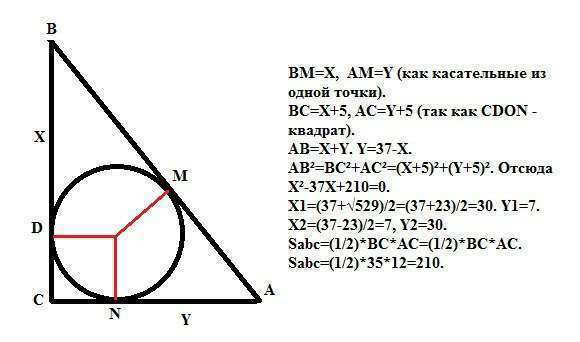
Пусть точки касания вписанной окружности с гипотенузой АВ - точка М, а с катетом АС - точка N.
BM=X, AM=Y (как касательные из одной точки).
ВС=Х+5, АС=Y+5 (так как CDON - квадрат).
АВ=Х+Y. Y=37-Х.
АВ²=ВС²+АС²=(Х+5)²+(Y+5)². Отсюда
Х²-37Х+210=0.
Х1=(37+√529)/2=(37+23)/2=30. Y1=7.
Х2=(37-23)/2=7, Y2=30.
Sabc=(1/2)*ВC*AC=(1/2)*BC*AC.
Sabc=(1/2)*35*12=210.
Более короткий путь: Расстояние от вершины С треугольника до точки, в которой вписанная окружность касается стороны, равно р=с, где р - полупериметр, а с - сторона, противолежащая вершине С (свойство). Тогда 5=р-37, отсюда р=42.
Тогда по формуле S=р*r = 42*5=210.