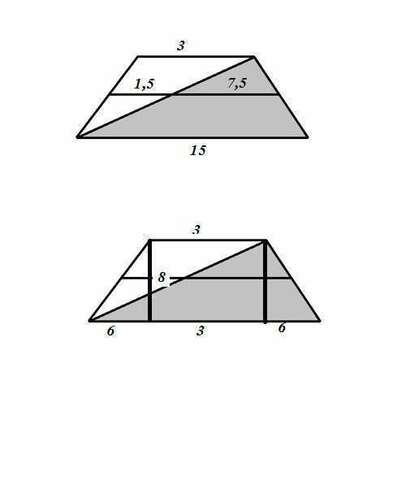
Диагональ трапеции делит ее на два треугольника. Отрезки средней линии трапеции являются средними линиями треугольников (см. рисунок)
По определению средней линии ее длина равна половине длины параллельного ей основания.
Следовательно, длины оснований трапеции равны:
1,5 х 2 = 3
7,5 х 2 = 15
Площадь трапеции равна произведению полусуммы оснований на высоту: S = (a+b)h/2
Отсюда высота трапеции: h = 2S/(a+b) = 2 x 72 / (15+3) = 8
Так как трапеция является равнобедренной, углы при ее основаниях попарно равны. Высоты, проведенные от верхнего основания к нижнему, делят нижнее основание на три отрезка: 6 + 3 + 6 = 15 (см.рисунок)
Длину боковой стороны найдем по теореме Пифагора из образовавшегося прямоугольного треугольника (боковая сторона - гипотенуза, катеты - высота и часть нижнего основания)
√8²+6² = √100 = 10