ПОМОГИТЕ С ГЕОМЕТРИЕЙ ЗА 99 БАЛЛОВ О1 - центр вписанной окружности треугольника abc ,а...

Question

ПОМОГИТЕ С ГЕОМЕТРИЕЙ ЗА 99 БАЛЛОВ
О1 - центр вписанной окружности треугольника abc ,а О2 - центр окружности, касающейся стороны BC и продолжения сторон AB и AC. Найдите расстояние между точками O1 и O2,если радиус описанной окружности треугольника ABC равен 6, а sin(BO1C)= (корень из 5)/3 .

Answer 1

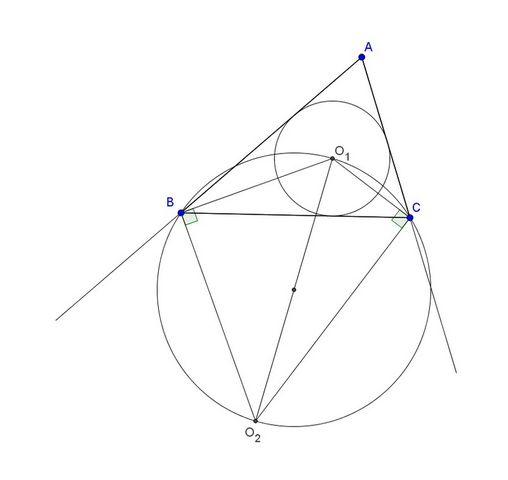
По условию О₂ - центр вневписанной окружности, т.е. О₂ лежит на пересечении биссектрис внешних углов треугольника ABC при углах B и С. Т.к. BO₁ и BO₂ - биссектрисы углов, сумма которых равна 180°, то ∠O₁BO₂=90°. Аналогично, ∠O₁СO₂=90°. Значит O₁BO₂C вписан в окружность c диаметром O₁O₂. Значит, по т. синусов для треугольника BO₁С получаем O₁O₂=BC/sin(BO₁C). Дальше, т.к. O₁ лежит на пересечении биссектрис углов ∠ABC и ∠AСB, то ∠BAC=2∠BO₁C-180°, и значит sin(∠BAC)=-sin(2∠BO₁C), т.е. по т. синусов для треугольника АBC получаем BC=-2Rsin(2∠BO₁C), где R - радиус окружности описанной около АBC. Итак,
O₁O₂=-2Rsin(2∠BO₁C)/sin(BO₁C)=-4Rcos(BO₁C)=4·6√(1-5/9)=16.

---

Comments

Спасибо большое вам