Найдите площадь фигуры, ограниченной заданными линиями: У=4-х(во второй степени) У=0 Х=0...

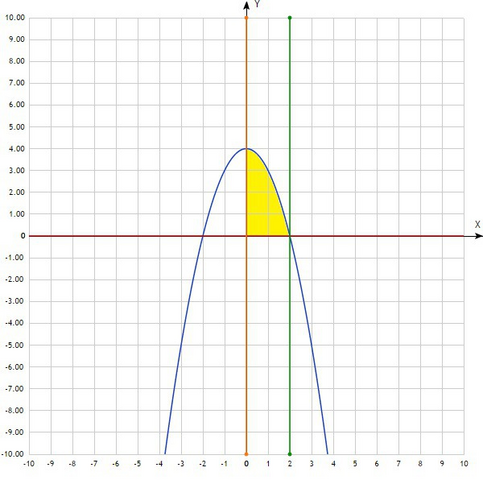
Чертим чертёж. Находим фигуру, площадь которой необходимо вычислить. Определяем пределы. Из рисунка видно, что искомая фигура лежит на отрезке [0;2] и ограничена графиком функции y=4-x² сверху и у=0 снизу, то есть расположена над осью ОХ. Площадь некоторой фигуры численно равна определённому интегралу, поэтому
$S= \int\limits^2_0 {(4-x^2)} \, dx=(4x- \frac{x^3}{3})|_0^2=4*2- \frac{2^3}{3}-0=8- \frac{8}{3}= \frac{16}{3}=5 \frac{1}{3}$ ед²