Решить систему двух уравнений с двумя переменными графически. Для этого нужно найти точки (точку) пересечения двух графиков функций, которые у тебя представленны, а для этого их нужно привести (преобразовать немного) и построить:
х+2у=0 (нужно 《перенести》 в другую часть выражения, за знак равенства х: т.е. от обеих частей выражения (левой от знака равенства и правой) отнять х)
5х+у=-18 (нужно 《перенести》 5х...)
2у=-х (после этого нужно сделать, чтоб слева от знака равенства был только у, т.е. обе части равенства нужно делить на 2)
у=-5х-18
у=-х/2
у=-5х-18
Т. к. это линейная функция (прямая) (и первая, и вторая), то строить её можно только по двум произвольным точкам (больше и не надо, чтобы построить прямую).
Точки первой:
пусть х=2
у=-2/2=1
Так первая точка первой фунции (2;-1)
Аналогично можно найти произвольную вторую точку графика первой функции, пусть, например, (-2;1)
Произвольные точки графика второй функции тоже аналагично можно найти, просто подставив любое значение х и подсчитав:
(-3;-3), (-4;2)
Строишь по двум точкам график каждой функции и находишь точку пересечения (общую точку) по полученному графику этих двух прямых.
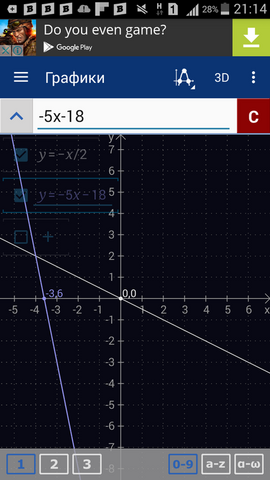
По графику точка пересечения: (-4;2).
Ответ: (-4;2).
Я тебе в программе нарисовал белым цветом график первой функции (у=-х/2) и синим график второй (у=-5х-18) (просто в школе их надо ещё и подписывать). Поставь 《+》 в комментариях, если получил скриншот программы, если не сложно.