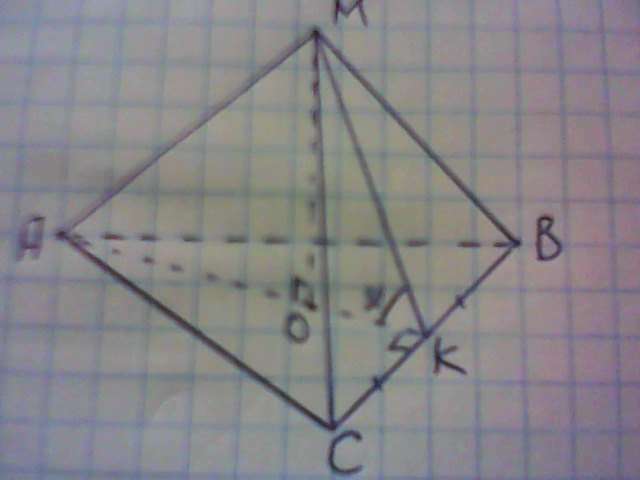
Пусть сторона основания пирамиды равна 2х, тогда ВК=СК=х.
АК - медиана. биссектриса, высота ΔАВС.
АК=√√АС²-СК²=√4х²-х²=х√3.
ОК=1/3 АК=х√3/3.
ΔΔМОК: tg30°=ОМ/ОК; tg30°=1/√3.
1/√3=OM/OK; ОМ - высота пирамиды, обозначим h.
1/√3=3h/x√3,
h=x/3.
Найдем площадь основания пирамиды S=АВ²√3/4=4х²√3/4=х²√3,
Вычислим объем пирамиды V=S·h/3.
8√3/3=x²√3/3 · x/3.
х³√3/9=8√3/3,
х=2∛3,
АС=2х=4∛3.
Ответ: 4∛3.