(рис.1)
а)АВ=АС=6 и CD=BE=2, то AE=AD=4
Рассмотрим треугольники АED и ABC.
∠ВАС-общий, АС/АD=AB/AE=6/4=3/2, следовательно треугольники подобны по 2-м пропорциональным сторонам и углу между ними.
Если треугольники пропорциональны, то их высоты, медианы и биссектрисы также будут пропорциональны
в ΔАВС проведем медиану АН
Пусть О-точка пересечения АН и DE
АН/АО=3/2, следовательно АО/ОН=2:1
Медианы точкой пересечения делятся в отношении 2:1, считая от вершины.
Если АО/ОН=2:1, то О-точка пересечения медиан.
Зная, что в равностороннем треугольнике медианы, высоты и биссектрисы равны, можно сказать,что О-точка пересечения биссектрис
Как раз центр вписанной окружности находится на пересечения биссектрис.
в равностороннем треугольнике центры вписанной и описанной окружностей совпадают, следовательно О-центр ΔАВС ч.т.д
б) заметим, что LD=LE-так как ΔАLD=ΔAEL по 2-м сторонам и углу между ними, следовательно ΔDLE-равнобедренный и LO-высота этого треугольника
СВ/DE=3/2; DE=3CB/2=2*6/3=4
DO=OE=DE/2=4/2=2
АО²=AD²-DO²=4²-2²=16-4=12
AO=√12=2√3
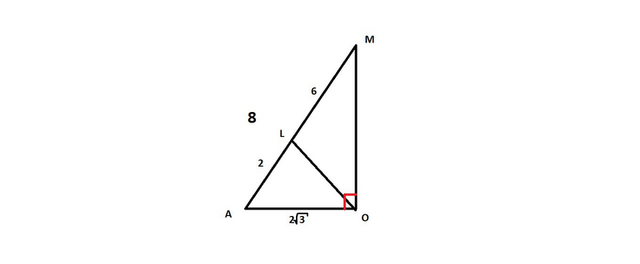
Теперь отдельно рассмотрим ΔLOM (рис.2)
cos∠MAO=AO/AM=2√3/8=√3/4
По теореме косинусов найдем ОL:
OL²=AL²+AO²-2*AL*AO*cos∠MAO
OL²=4+12-2*2*2√3*√3/4
OL²=16-8*3/4=16-6=10
OL=√10
Sсеч=SΔdle=DE*LO/2=4*√10/2=2√10
отв: 2√10