№1Основание пирамиды-равнобедренный прямоугольный треугольник с гипотенузой 4 корень из2...

Question

№1Основание пирамиды-равнобедренный прямоугольный треугольник с гипотенузой 4 корень из2 см.Боковые грани,содержащие катеты треугольника,перпендикулярны к плоскости основания,а третья грань наклонена к ней под углом 45 градусов.
а)Найдите длины боковых ребер пирамиды
б)Найдите площадь боковой поверхности пирамиды.

№2 Ребро куба ABCDA1E1C1 равно a.Постройте сечение куба,проходящее через точку С и середину ребраAD параллельно прямой DA1 и найдите площадь этого сечения.

Пожалууйста помогите очень нужно на сегодня!!!!

Answer 1

№1  АВ, ВС катеты
Так как гипотенуза известна, то катеты можно найти
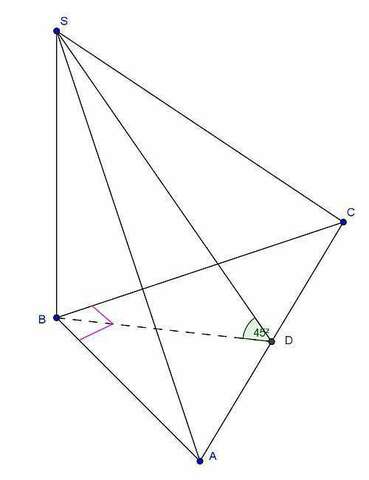
Так как боковые грани , содержащие катеты треугольника, перпендикулярны к плоскости основания, то они пересекаются по SВ⊥(АВС)
Пусть D - середина гипотенузы АС. Докажите, что BD⊥AC, а тогда и SD⊥АС (т. о трех перпендикулярах)
След, угол SDB - линейный угол двугранного угла и равен 45°

АВ, ВС катеты
Так как гипотенуза известна, то катеты можно найти
Потом найти ВD, затем найти SA и SD
Затем 2 боковых ребра

 

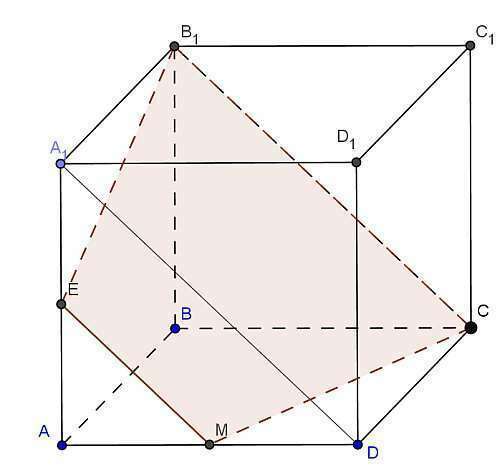
№2  Если плоскость имеет с другой плоскостью две общие точки, то эти плоскости пересекаются по прямой, проходящей через эти две точки = > секущая плоскость пересекает нижнюю грань по прямой См
Так как плоскость сечения параллельна DA1, лежащей в грани АА1D1D, то она пересекает эту грань по прямой, параллельной DA1

 

 

---

---