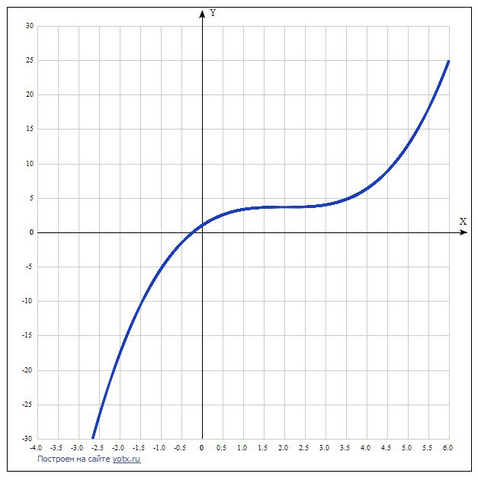
Дана функция y=(1/3)x^3-2x^2+4x+1.
Производная равна (1/3)*3х² - 2*2х + 4 = х² - 4х + 4.
Находим критические точки, приравняв производную нулю:
х² - 4х + 4 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:D=(-4)^2-4*1*4=16-4*4=16-16=0;
Дискриминант равен 0, уравнение имеет 1 корень:x=-(-4/(2*1))=-(-2)=2.
Исследуем поведение производной вблизи критической точки.
х = 1.5 2 2.5
у' =x^2-4x+4 0.25
0 0.25.
Производная не меняет знак - значит, нет экстремума.
Так как производная положительна, то функция на всём числовом промежутке возрастающая.