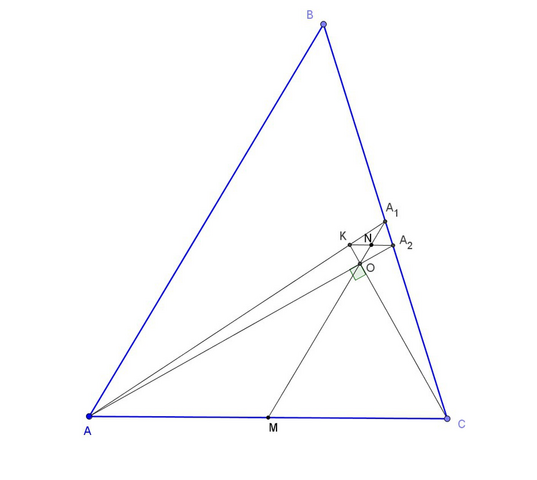
Пусть KC и AA₂ пересекаются в О. а прямая A₁O пересекает AC в M. Тогда, т.к. AKA₂С - трапеция, то M - середина AC. Значит, MA₁ - средняя линия треугольника ABC, т.е. MA₁||AB, откуда ∠AOM=∠BAO=∠OAM, т.е. MO=AM=MC, значит ∠AOC опирается на диаметр AC, т.е. ∠AOC=90°. Длины AC и BC в условии не нужны.
P.S. То, что M является серединой AC - известный факт, верный для любой трапеции. Доказать его можно так: Если N - точка пересечения A₁M и KA₂, то из пар подобных треугольникв получаем:
KN/MC=ON/OM=NA₂/AM, откуда KN/NA₂=MC/AM;
KN/AM=A₁N/A₁M=NA₂/MC, откуда KN/NA₂=AM/MC.
Значит MC/AM=AM/MC, т.е. MC=AM.