В параллелограмме ABCD отмечена точка M-середина стороны BC. отрезки BD и AM пересекаются...

Question

В параллелограмме ABCD отмечена точка M-середина стороны BC. отрезки BD и AM пересекаются в точке K. найдите BK, если BD=12

Answer 1

Соединим середину стороны АД и вершину С прямой СН. СН║АМ т.к. МС║АН и МС=АН. Прямые СН и ВД пересекаются в точке Р.
В тр-ке ВРС КМ - средняя линия, значит ВК=КР.
Тр-ки АВМ и ДСН равны по трём равным сторонам., значит ВК=РД.
ВД=ВК+КР+РД=3BK ⇒ ВК=ВД/3=12/3=4 - это ответ.

Answer 2

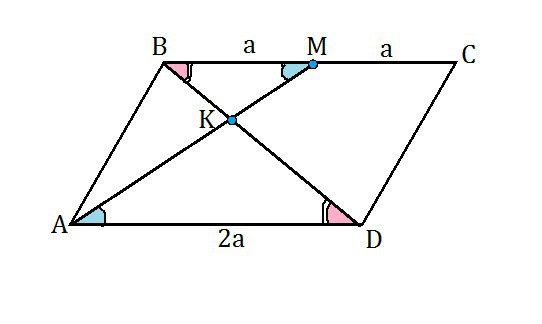
Пусть ВМ=МС=а.
Тогда, поскольку противоположные стороны параллелограмма равны и параллельны,  АD=2a.
Треугольники ВКМ и АКD подобны по трем углам: равны вертикальные углы при К и накрестлежащие при пересечении параллельных прямых секущими ВD и АМ.
Коэффициент подобия k=AD:BC=2a:a= 2.
Отсюда КD:BK=2:1⇒
BK+KD= 3 части. 
12:3=4
ВК=1 часть
ВК=4

---