План исследование функции.
1.Определить вид функции, если возможно (указать её название и название графика, если определили вид) - это парабола.
2. Найти область определения функции (множество значений аргумента х, на котором данная функция определена) - Квадратичная функция, заданная формулой y = ax2 + bx + c, определена при всех вещественных значениях аргумента x. Ее областью определения является множество R.
В данной параболе b = 0,
3. Найти область значения функции (множество значений функции у) - При a > 0 областью значений функции y будет промежуток [-D/4a;∞).
4. Найти нули функции (точки пресечения с осью х) если возможно, для чего приравнять нулю у=0 (выражение, соответствующее формуле функции).
График функции пересекает ось X при f = 0
значит надо решить уравнение:
x²−2=0Точки пересечения с осью X:
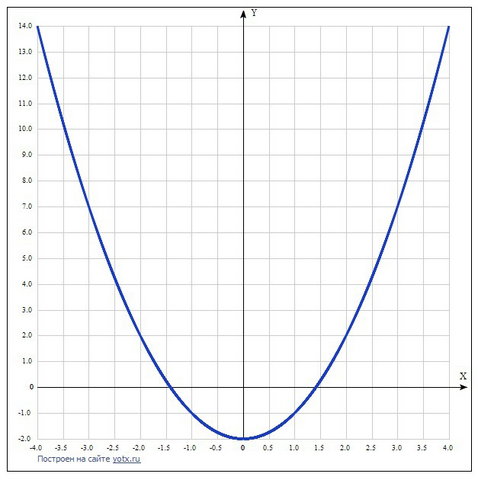
x1 = √2, x2 = -√2.
Численное решение
x1=1.41421356237, x2=−1.41421356237.5. Определить, при каких значениях аргумента х значения функции у>0, при каких значениях аргумента у <0. <br>График пересекает ось Y, когда x равняется 0:
подставляем x = 0 в x^2 - 2.
Y(0) = 0²−2 = -2
Точка: (0, -2)
6. Выяснить, является ли функция четной (симметричной относительно оси ординат) или нечетной (симметричной относительно начала координат), или заведомо не является ни четной, ни нечетной.
Так как в формуле нет коэффициента b, то парабола симметрична оси Оу. Функция функция является чётной.
7. Построить таблицу значений данной функции - в приложении.
8. Определить, является ли функция возрастающей (убывающей) или указать промежутки возрастания (убывания).
Так как вершина данной параболы находится на оси Оу, то при отрицательных значениях аргумента функция убывающая, а при положительных - возрастающая.
9. Начертить график, отметив в координатной плоскости точки, координаты которых соответствуют парам (х,у), полученным в таблице, и соединив их плавной (прямой) линией.