Функция задана формулой g(x)=35/(x^2 -9) Как построить данную функцию?(понятно, что она...

Question

Функция задана формулой
g(x)=35/(x^2 -9)
Как построить данную функцию?(понятно, что она сдвинется на 9 в право, не понятно как изобразить 35/х^2)

Comments

она не сдвигается на 9, т.к. вычитание в знаменателе. Тут типо полное исследованеи нужно, где возрастает/убывает/ точки перегиба и потом по точкам

---

Но, если f(x)=(x +/- a), то график сдвигается по оси х с противоположным знаком, а если f(x)=(x +/- b) +/- a, тогда сдвигается по оси у и знак не меняется

---

у тебя же не такого вида уравнение, тут такое уже не прокатит. Я просто посмотрела онлайн график этой ф-ции там действительно нет никаких сдвигов

---

Я тоже посмотрела его. Но как тогда "выйти" на стандартный вид графика?

---

мы просто делали полное исследование + эскиз графика

Answer 1

1. Область определения х∈(-∞;-3)U(-3;3)U(3;+∞).
2. Находим производную
  
3. Находим точки, в которых производная равна 0.
   у`=0    ⇒  x=0
4. Находим промежутки возрастания и убывания, для этого на области определения отмечаем точки, в которых производная равна 0 и расставляем знаки производной.

__+___(-3)___+__(0)___-___(3)__-___

5. На (-∞;-3) и на (-3;0) функция возрастает.
   На (0;3) и на (3;+∞) функция убывает.
х=0 - точка локального максимума функции, так как производная меняет знак с + на -.
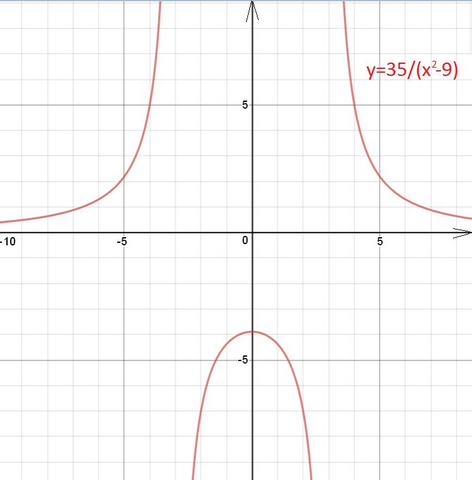
График функции см. на рисунке.

Этот график не может быть получен из графика у=35/х² так как имеет совершенно другой вид у=35/(х-3)(х+3) 

---