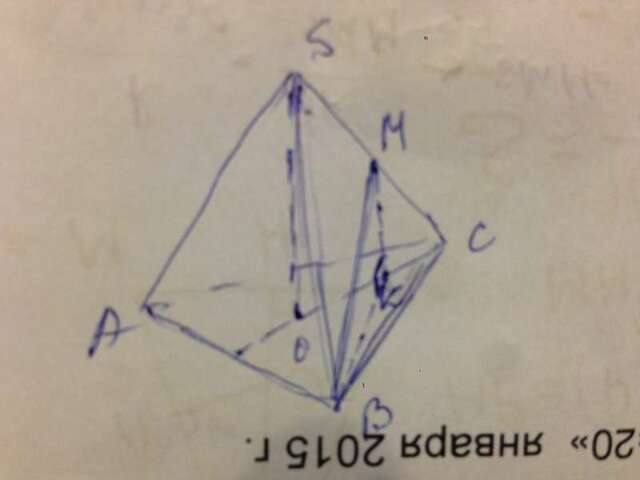
В правильной пирамиде SABC SO - высота пирамиды. СО - радиус описанной около основания окружности. СО=а√3/3=2√3·√3/3=2.
СО - проекция ребра SO на плоскость основания. Опустим высоту МК на отрезок СО. В тр-ке SOC МК - средняя линия т.к. МК║SO и SM=MC, значит МК=SO/2.
SO²=SC²-CO²=32-4=28.
SO=2√7.
MK=√7.
Так как в тр-ке ВМК МК перпендикулярна плоскости основания, нужно найти угол МВК.
В тр-ке BSC ВМ - медиана. Формула медианы: m²=(2b²+2c²-a²)/2,
ВМ²=(2ВS²+2ВС²-SC²)/2=(SC²+2BC²)/2=(32+24)/2=28,
ВМ=√28=2√7.
В тр-ке ВМК sin(MBK)=МК/ВМ=(√7)/(2√7)=1/2.
∠MBK=30° - это ответ.