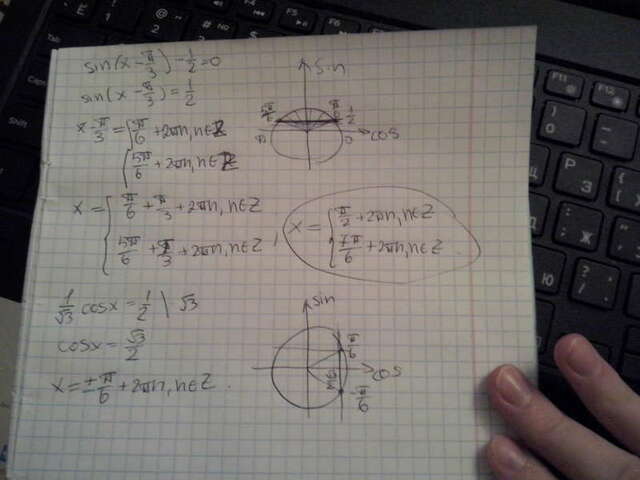1. Перенесём 1/2 в правую часть, таким образом выразим синус:
sin(x-π/3)=1/2
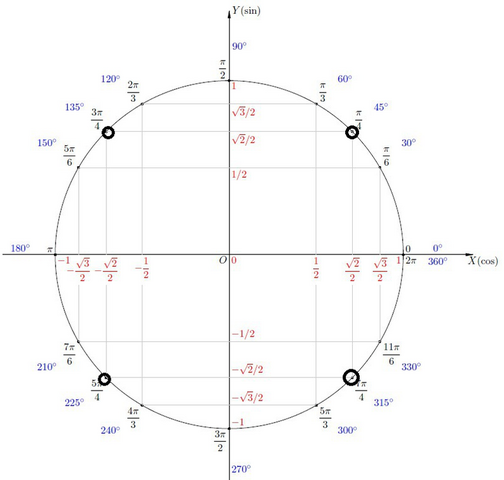
Находим аргумент синуса. Чтобы не запоминать формулы, можно просто вспомнить тригонометрический круг (его прилагаю). Смотрим, где синус равен 1/2. Причём стоит быть внимательным, т.к. мы находим по тригонометрическому кругу АРГУМЕНТ синуса "х-π/3", а не "х". Итак, аргумент синуса равен π/6 и 5π/6, если синус равен 1/2.
Т.е.:
х-π/3=π/6
x-π/3=5π/6
Отсюда х принимает два значения:
х=π/6+π/3=π/6+2π/6=3π/6=π/2+2πn, n∈R (n-целое число)
x=5π/6+π/3=5π/6+2π/6=7π6+2πn, n∈R
+2πn, n∈R появляется, когда ровно через круг значение х попадает в эту же точку.
2. Умножим обе части уравнения на √3:
cosx=√3/2
Смотри на тригонометрический круг. Аргумент косинуса, равного √3/2, будет принимать значение π/6+2πn, n∈R и -π/6+2πn, n∈R.
Если есть какие-то вопросы по данной задаче-задавай в комментариях)
Решение во вложении.