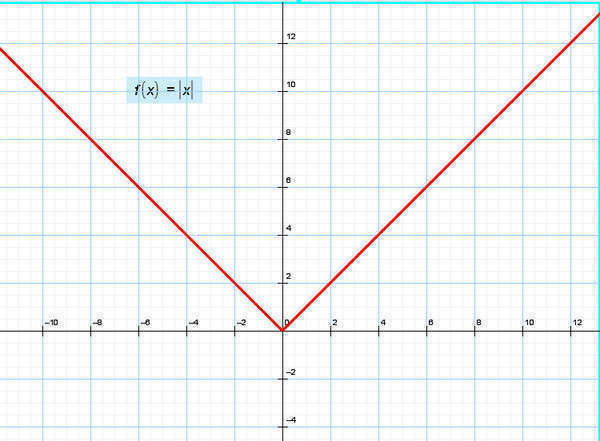
Необходимо знать, что такое модуль числа или выражения.
Модуль положительного числа - есть само положительное число, например |6|=6. Модуль отрицательного числа равен этому же числу, но с плюсом, например: |-7|=7. Это видно из рисунка, который я прилагаю.
В связи с эти выражение под знаком модуля может быть как положительным, так и отрицательным, т.е.:
|x|=b
х=b или -x=b.
В связи с этим у нас есть два развития событий: или выражение под модулям отрицательное, или же оно положительное. Раскроем модуль, когда выражение под ни положительное:
4*(2-х)≤12
Раскроем скобки:
8-4х≤12
Перенесём всё, что с х направо, а известные числа-налево:
8-12≤4х
-4≤4х
Разделим обе части неравенства на 4, таким образом выразив х:
-1≤х
Или: х≥-1.
Теперь выражение под модулем раскроем с отрицательным знаком:
4*(-(2-х))≤12
4*(-2+х)≤12
-8+4х≤12
Всё, что с х оставим в левой части, а известные числа перенесём в правую часть:
4х≤12+8
4х≤20
Разделим обе части неравенства на 4, таким образом выразив х:
х≤20
У нас получаются 2 ответ:
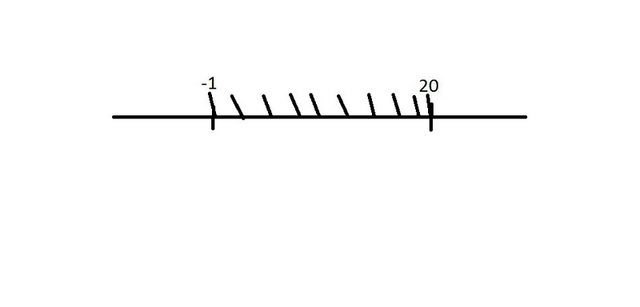
х≥-1 и х≤20.
Теперь нам нужно объединить эти два ответ. На рисунке я пояснила, почему получился такой ответ:
х∈[-1;20].