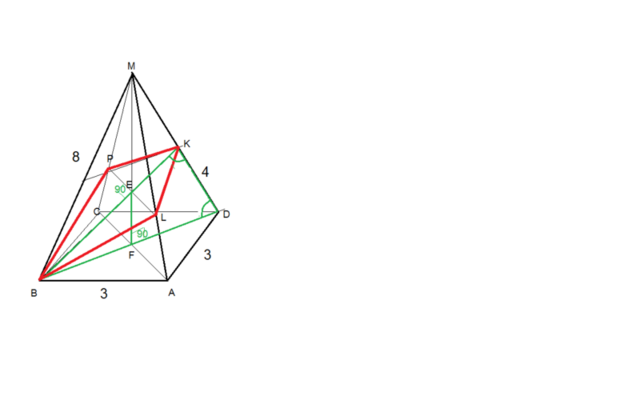
искомое сечение - симметричный четырехугольник BPKL
диагонали PL , BK пересекаются под углом 90 град
по условию
стороны основания AB=BC=CD=AD =3
боковые ребра MA=MB=MC=MD =8
точка К - середина ребра MD ; KD = MD /2 = 8/2=4
ABCD -квадрат
диагональ AC = BD = 3√2
пересечение диагоналей точка F : BF =FD = BD/2 =3√2 /2 =1.5√2
BK - медиана треугольника MBD
длина медианы BK = 1/2 √(2 BM^2 +2 BD^2 - MD^2 ) =1/2 √(2*8^2 +2*(3√2)^2 - 8^2 ) =5
по теореме косинусов
cos KBD = ( KD^2 - (BK^2+BD^2) )/ (-2*BK*BD)= ( 4^2 - (5^2+(3√2)^2) )/ (-2*5*3√2)= 9/(10√2)
MF - высота
треугольник EBF - прямоугольный
BE = BF / cos KBD = 1.5√2 / [ 9/(10√2)] = 10/3
по теореме Пифагора EF =√(BE^2 - BF^2) =√( (10/3)^2 - (1.5√2)^2) =√238/6
MF - высота
треугольник MFB - прямоугольный
по теореме Пифагора MF =√( MB^2 -BF^2) =√( 8^2- (1.5√2)^2 ) =√238/2
ME =MF -EF =√238/2- √238/6= √238/3
треугольники MPL ~ MCA подобные
PL / AC = ME /MF ; PL = AC * ME /MF = 3√2 * √238/3 /√238/2 =2√2
площадь сечения(четырехугольника BPKL)
Sс = PL*BK *sin
Ответ 5√2