В правильной четырех-угольной пирамиде MABCD c вершиной M стороны основания равны 9/2, а... - Все ответы

99 просмотров

В правильной четырех-угольной пирамиде MABCD c вершиной M стороны основания равны 9/2, а боковые ребра равны 12. Найти площадь сечения пирамиды, плоскостью, проходящей через точку С и середину ребра AM параллельно прямой BD это С2, будет лучше если с решинием

Математика Fizikmaster_zn (158 баллов) 11 Март, 18 | 99 просмотров

Дан 1 ответ

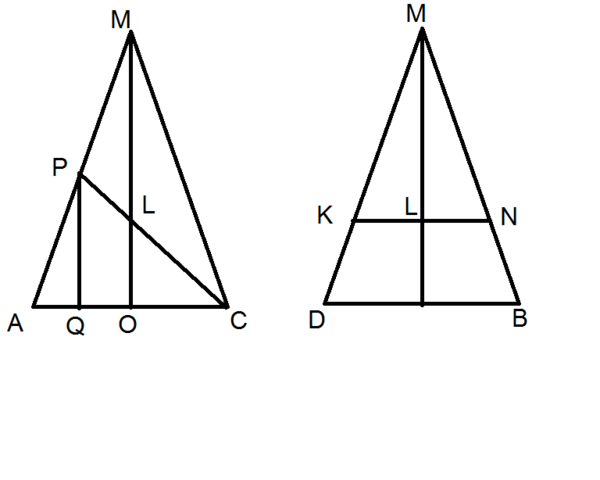
На вложенном рисунке диагональные сечения пирамиды с введенными обозначениями:

P - середина AM

O - центр основания, она же основание высоты

Q - проекция P на основание

L - пересечение высоты пирамиды и CP

K и N - точки пересечения ребер MD и MB плоскостью сечения (по условию эта прямая параллельна BD).

Теперь рассмотрим длины некоторых отрезков:

|AC| = |BD| = $\frac{9}{\sqrt{2}}$

Из подобия треугольников APQ и AMO

$|AQ| = \frac{|AO|}{2} = \frac{|AC|}{4} = \frac{9\sqrt{2}}{8}$

$|MO|= \sqrt{12^2-(\frac{9\sqrt{2}}{4})^2}}=\sqrt{\frac{1071}{8}}=3\sqrt{\frac{119}{8}}$

Достаточно очевидно, что

$\frac{|QC|}{|OC|} = \frac{3}{2}$

из подобия треугольников CPQ и CLO имеем:

$\frac{|PQ|}{|LO|} = \frac{QC}{OC} = \frac{3}{2}$

следовательно:

$|LO| = \frac{2}{3}|PQ| = \frac{2}{3}(\frac{1}{2}|MO|) = \frac{|MO|}{3} = \sqrt{\frac{119}{8}}$

Из подобия треугольников MDB и MKN:

$|KN| = \frac{|ML|}{|MO|}|DB| = \frac{2}{3}|DB| = \frac{9\sqrt{2}}{3}$

$|PC| = \sqrt{|PQ|^2+|QC|^2} = \sqrt{\frac{9*119}{4*8}+\frac{9*81}{16*2}} =\\ = \sqrt{\frac{900}{16}}=\frac{15}{2}$

Вполне очевидно, что BD перпендикулярно плоскости ACM

Следовательно и KN перпендикулярно ей, а значит и прямой PC

А т.к. диагонали четырехугольника CKPN перпендикулярны, то его площадь равна произведению длин этих диагоналей...

$S = |PC|*|KN| = \frac{15}{2}*\frac{9\sqrt{2}}{3}=\frac{45\sqrt{2}}{2}\approx 31.82$

hELFire_zn (11.5k баллов) 11 Март, 18