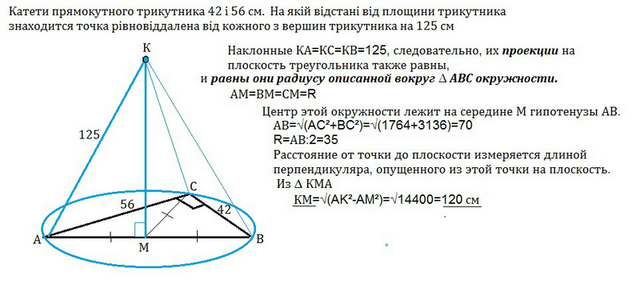
Катеты прямоугольного треугольника 42 и 56 см. На каком расстоянии от плоскости треугольника находится точка, равноудаленная от вершин треугольника на 125 см.
Пусть данный треугольник АВС, угол С=90º. Точка К удалена от А, В, С на 125 см.
Наклонные КА=КС=КВ=125 см, следовательно, их проекции на плоскость треугольника равны радиусу описанной вокруг ∆ АВС окружности.
АМ=ВМ=СМ=R
Центр этой окружности лежит на середине М гипотенузы АВ.
АВ=√(AC²+BC²)=√(1764+3136)=70 см
R=АВ:2=35
Расстояние от точки до плоскости измеряется длиной перпендикуляра, опущенного из этой точки на плоскость.
Из ∆ КМА
КМ=√(AK²-AM²)=√14400=120 см