помогите решить геометрию пожалуйста с рисунками

Question

Дан 1 ответ

Правильный ответ

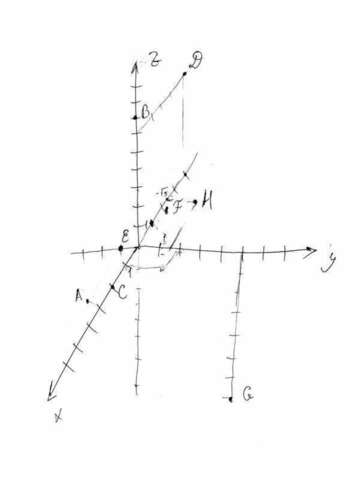
№1.

а) на оси абсцисс лежат точки, у которых ордината и аппликата равны нулю. То есть вторая и третья координаты равны 0. Этому условию удовлетворяет только точка С (2;0;0).

б) на оси аппликат лежат точки, у которых абсцисса и ордината равны нулю. То есть первая и вторая координаты равны нулю. Это только точка В (0;0;-7). См. рисунок

в) На плоскости ОХУZ лежат только точки. у которых абсцисса равна 0. Это значит, что первая координата равна нулю. Этому условию удовлетворяют точчки B(0;0;-7), E(0;-1;0),G(0;5;-7)

№2

а) Сначала напишем векторы. Вычитаем из конечной координаты начальную

$\vec{AB}=\{2-1;3-6;-1-2\};\quad\vec{BC}=\{-3-2;4-3;5-(-1)\}$

$\quad\vec{CA}=\{1-(-3);6-4;2-5\}$

$\vec{AB}=\{1;-3;-3\};\quad\vec{BC}=\{-5;1;6\}\quad\vec{CA}=\{4;2;-3\}$

Согласно этим вычислениям разложим полученные векторы по координатным векторам

$\vec{AB}=\vec i-3*\vec j-3*\vec k$

$\vec{BC}=-5*\vec i+\vec j+6*\vec k$

$\vec{CA}=4*\vec i+2*\vec j-3*\vec k$

Периметр находится так. Найдем длину каждого вектора, потом сложим все длины.

$|\vec{AB}|=\sqrt{1^2+(-3)^2+(-3)^2}=\sqrt{1+9+9}=\sqrt{19}$

$|\vec{BC}|=\sqrt{(-5)^2+1^2+6^2}=\sqrt{25+1+36}=\sqrt{62}$

$|\vec{CA}|=\sqrt{4^2+2^2+(-3)^2}=\sqrt{16+4+9}=\sqrt{29}$

Периметр треугольника равен

$P_{\Delta}=\sqrt{19}+\sqrt{62}+\sqrt{29}$

№ 3.

а) Сначала напишем векторы. Вычитаем из конечной координаты начальную

$\vec{AB}=\{2-1;3-6;-1-2\};\quad\vec{BC}=\{-3-2;4-3;5-(-1)\}$

$\quad\vec{CA}=\{1-(-3);6-4;2-5\}$

$\vec{AB}=\{1;-3;-3\};\quad\vec{BC}=\{-5;1;6\}\quad\vec{CA}=\{4;2;-3\}$

Согласно этим вычислениям разложим полученные векторы по координатным векторам

$\vec{AB}=\vec i-3*\vec j-3*\vec k$

$\vec{BC}=-5*\vec i+\vec j+6*\vec k$

$\vec{CA}=4*\vec i+2*\vec j-3*\vec k$

Периметр находится так. Найдем длину каждого вектора, потом сложим все длины.

$|\vec{AB}|=\sqrt{1^2+(-3)^2+(-3)^2}=\sqrt{1+9+9}=\sqrt{19}$

$|\vec{BC}|=\sqrt{(-5)^2+1^2+6^2}=\sqrt{25+1+36}=\sqrt{62}$

$|\vec{CA}|=\sqrt{4^2+2^2+(-3)^2}=\sqrt{16+4+9}=\sqrt{29}$

Периметр треугольника равен

$P_{\Delta}=\sqrt{19}+\sqrt{62}+\sqrt{29}$

№4.

Скалярное произведение. Сначала вычислим просто чему равно $2\vec a+\vec b$

$2\vec a+\vec b=(2*1+2;2*0-1;2*3+1)=(4;-1;7)$

Теперь можно найти и скалярное произведение. Для этого просто нужно перемножить координаты векторов $2\vec a+\vec b$ и $\vec a$ .

$(2\vec a+\vec b)*\vec a=(4*1;-1*0;7*3)=(4;0;21)$

Ответ: $(4;0;21)$

5) Найдем сначала

$\vec {AB}=\{4-(-1);2-2;2-2\}=\{5;0;0\}$

$\vec {CD}=\{1-(-4);-7-(-2);2-2\}=\{5;-5;0\}$

Вычислим длины этих векторов

$|\vec {AB}|=\sqrt{5^2+0^2+0^2}=5$

$|\vec {CD}|=\sqrt{5^2+(-5)^2+0^2}=5\sqrt{2}$

Вычислим скалярное произведение векторов $\vec {AB}$ и $\vec {CD}$ .

$\vec {AB}*\vec {CD}=5*5+0*(-5)+0*0=25$

Косинус угла между этими векторами вычисляется следующим образом

$\cos(\vec{AB},\vec{CD})=\frac{\vec{AB}*\vec{CD}}{|\vec{AB}|*|\vec{CD}|}=\frac{25}{5*5\sqrt{2}}=\frac{1}{\sqrt{2}}$

$\arccos\left(\frac{1}{\sqrt{2}}\right)=\frac{\pi}{4}$

или 45 градусов.

Ответ: 45 градусов.

bearcab_zn (114k баллов) 11 Март, 18