Общая схема исследования и
построения графика функции
1. Найти область определения
функции и область значений функции, выявить точки разрыва, если они есть.
Область определения функции - вся числовая ось.
D(x) = R.
2. Выяснить, является ли функция
четной или нечетной.
f(-x) = -(x^3-15x)/3.
Функция является нечетной. Нечетность функции указывает на симметрию графика относительно начала координат.
3. Выяснить, является ли функция
периодической.
Функция непериодическая.
4. Найти точки пересечения графика
с осями координат (нули функции). С осью Ох: у = 0.
(x^3-15x)/3 = 0.
x(x^2-15) = 0.
Имеем 3 корня: х = 0, х = √15, х = -√15.
5. Найти асимптоты графика. Их нет.
6. Вычислить производную функции f'(x)
и определить критические точки.
f'(x) = (1/3)*3x^2 - 5 = x² - 5.
Критические точки - при f'(x) = 0:
x² - 5 = 0, х = +-√5.
7. Найти промежутки монотонности
функции.
Исследуем производную вблизи критических точек:
х =
-2.5 -2.23607 -2
2 2.23607 2.5
y' = x^2-5 1.25 0
-1 -1
0 1.25.
Где производная положительна, там функция возрастает. Где отрицательна - там функция убывает.
Возрастает на промежутках
(-oo, -sqrt(5)] U [sqrt(5), oo)
Убывает на промежутках
[-sqrt(5), sqrt(5)]
8. Определить экстремумы функции f(x).
Их видно по пункту 7. Где производная меняет знак с + на - это максимум функции, где с - на + там минимум.
Минимум функции в точке x = √5.
Максимумы функции в точке x=−√5.
9. Вычислить вторую производную f''(x).
f''(x) = 2х.
Находим точку перегиба графика 2х = 0, х = 0.
10. Определить направление
выпуклости графика и точки перегиба.
Вогнутая на промежутке [0, oo).
Выпуклая на промежутке (-oo, 0].
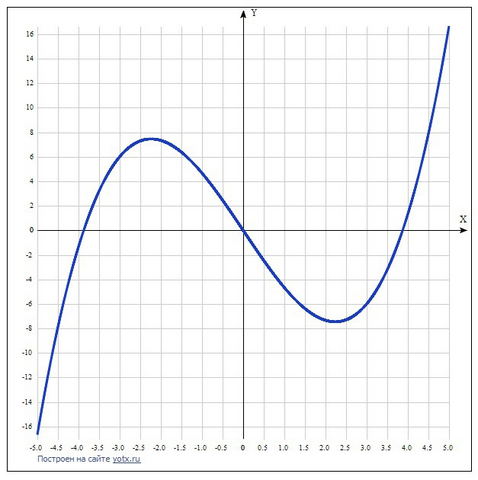
11. Построить график, используя
полученные результаты исследования. В приложении.