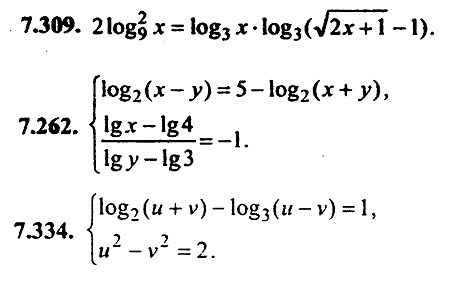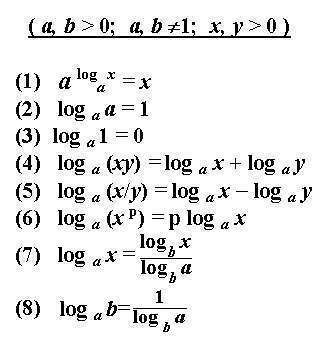Логарифмы. 7.309 - решить уравнение. 7.262, 7.334 - решить системы уравнений. Объясняйте...

Question

Логарифмы.
7.309 - решить уравнение.
7.262, 7.334 - решить системы уравнений.
Объясняйте как можно больше, пожалуйста и как можно более пошагово.
Пишите, пожалуйста, какую конкретно формулу где вы использовали из картинки 2. Напр.: "тут я исп. формулу (3)"
Пишите номер решаемого 7.334 ...

---

---

Answer 1

7.309
2㏒²₉x=㏒₃x*㏒₃(√(2x+1)-1)
Определяем область допустимых значений логарифмов:
х>0
√(2x+1)-1>0    √(2x+1)>1  2x+1>1  2x>1-1  2x>0  x>0
то есть х∈(0;+∞)

Далее приводим логарифмы к одинаковому основанию, так как в первом логарифме основание 9. 9 можно представить как 3². Из свойства логарифмов: ㏒ₐⁿb=1/n*㏒ₐb
2*㏒²₃²х=2*(1/4)*㏒²₃х=1/2*㏒²₃х

1/2*㏒²₃х=㏒₃х*㏒₃(√(2х+1)-1)
㏒²₃х/㏒₃х=2*㏒₃(√(2х+1)-1)
Далее используем формулу (6) для логарифма справа от равно
㏒₃х=㏒₃(√(2х+1)-1)²
x=(√(2x+1)-1)²
x=(√(2x+1))²-2√(2x+1)+1
x=2x+1-2√(2x+1)+1
x-2x-2=-2√(2x+1)
x+2=2√(2x+1)
(x+2)²=4(2x+1)
x²+4x+4=8x+4
x²+4x-8x+4-4=0
x²-4x=0
x(x-4)=0
x=0 -  не принадлежит ОДЗ, поэтому не является корнем 
x-4=0
x=4