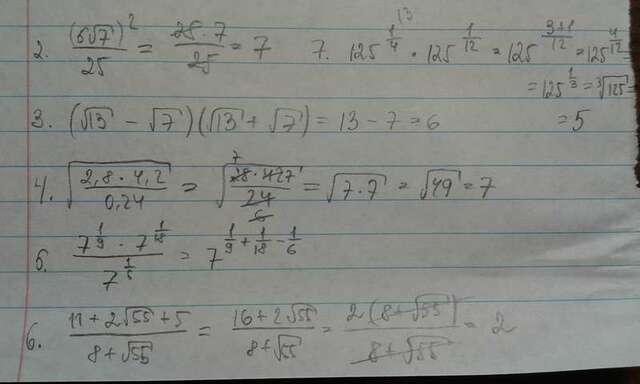Помогите пожалуйста!!! Решите все уравнения с корнями, кроме 1.

2. Числитель возводим в квадрат - корень уходит.
3. Сворачиваем по формуле сокращенного умножения - разность квадратов.
4. Всё вносим под один корень, потом умножаем числитель и знаменатель на 100.
5. Здесь дробные степени.
6. Раскладываем числитель по формуле сокращенного умножения - квадрат суммы, потом выносим 2 и сокращаем.
7. Опять дробные показатели. А корень третьей степени из 125 это 5, так как 5 в кубе = 125.

2) $\frac{(5 \sqrt{7} )^{2}}{25} = \frac{5^{2} \sqrt{7}^{2} }{5^{2}} = \sqrt{7}^{2} = 7$
3) $( \sqrt{13} - \sqrt{7} )( \sqrt{13} + \sqrt{7} ) = \sqrt{13}^{2} - \sqrt{7}^{2} = 13 - 7 = 6$
4) $\frac{ \sqrt{2,8} \sqrt{4,2}}{ \sqrt{0,24}} = \frac{\sqrt{2,8 * 4,2}}{\sqrt{0,24}} = \sqrt{\frac{2,8 * 4,2}{0,24}} = \sqrt{\frac{28 * 42 * 100}{24 * 100}} = \sqrt{\frac{28 * 42}{24}} = \sqrt{\frac{7 * 2^{2} * 2 * 3 * 7}{2^{3} * 3}}}$ = $\sqrt{\frac{7 * 2^{2} * 2 * 3 * 7}{2^{3} * 3}}} = \sqrt{7^{2}} = 7$
5) $\frac{ \sqrt[9]{7} \sqrt[18]{7}}{ \sqrt[6]{7}} = \frac{ 7^{ \frac{1}{9}} 7^{ \frac{1}{18}}}{ 7^{ \frac{1}{6}}} = 7^{ \frac{1}{9} + \frac{1}{18} - \frac{1}{6}} = 7^{0} = 1$
6) $\frac{( \sqrt{11} + \sqrt{5} )^{2}}{8 + \sqrt{55}} = \frac{ \sqrt{11}^{2} + 2\sqrt{11}\sqrt{5} + \sqrt{5}^{2}}{8 + \sqrt{55}} = \frac{ 11 + 2\sqrt{55} + 5}{8 + \sqrt{55}} = \frac{ 16 + 2\sqrt{55}}{8 + \sqrt{55}} = \frac{ 2(8 + \sqrt{55})}{8 + \sqrt{55}} = 2$
7) $3 * \sqrt[4]{125} * \sqrt[12]{125} = 3 * 125^{ \frac{1}{4}} * 125^{\frac{1}{12}} = 3 * 125^{\frac{1}{3}} = 3 * \sqrt[3]{125} = 3 * \sqrt[3]{5^{3}}$ = 3 * 5 = 15
8) $\frac{12 * \sqrt[9]{m} * \sqrt[18]{m} }{\sqrt[6]{m}} = \frac{12 * m^{ \frac{1}{9}} * m^{ \frac{1}{18}} }{m^{ \frac{1}{6}}} = 12 * m^{\frac{1}{9} + \frac{1}{18} - \frac{1}{6}} = 12 * m^{0} = 12 * 1 = 12$
9) $\frac{ \sqrt{m}}{ \sqrt[4]{m} \sqrt[12]{m}} = \frac{m^{ \frac{1}{2}}}{ m^{\frac{1}{4}} m^{\frac{1}{12}}} = m^{\frac{1}{2} - \frac{1}{4} - \frac{1}{12}} = m^{\frac{1}{6}} = \sqrt[6]{m} = \sqrt[6]{4096} = \sqrt[6]{2^{12}} = 2^{2}$ = 4
10) $\sqrt[4]{64} * \sqrt[12]{64} = 64^{\frac{1}{4}} * 64^{\frac{1}{12}} = 64^{\frac{1}{4} + \frac{1}{12}} = 64^{\frac{1}{3}} = \sqrt[3]{64} = \sqrt[3]{2^{6}} = 2^{2} = 4$
P.S. поставьте мой ответ как самый лучший, пожалуйста :)