Используя свойство возрастания или убывания функции y=sinx сравнить числа: sin 7п/10 и...

Question

Дан 1 ответ

Правильный ответ

Синус на промежутке $[ -\frac{\pi}{2} ; \frac{\pi}{2} ]$ возрастает, а на промежутке $[ \frac{\pi}{2} ; \frac{3\pi}{2} ]$ - убывает

так как функция синуса периодична с периодом $2\pi$ , то:
$[ -\frac{\pi}{2}+2\pi n ; \frac{\pi}{2}+2\pi n ],n\in Z$ - промежутки возрастания синусоиды
и
$[ \frac{\pi}{2}+2\pi n ; \frac{3\pi}{2}+2\pi n ],n\in Z$ - промежутки убывания синусоиды

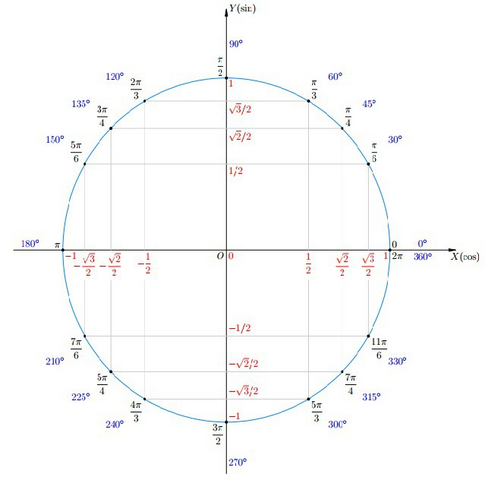
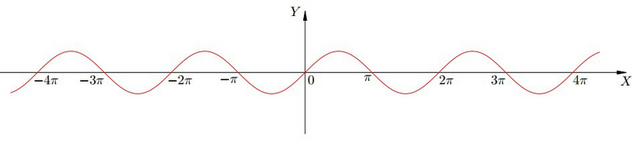
Что бы в этом убедится, предлагаю внимательно рассмотреть график синусоиды и/или тригонометрический круг

точка $- \frac{\pi}{2}$ и точка $\frac{3\pi}{2}$ - одна и та же точка на тригонометрическом круге

Что бы ответить на вопросы задания, осталось посмотреть, в какие промежутки попадают углы:
$sin( \frac{7\pi}{10} )$ и $sin( \frac{13\pi}{10} )$
у нас углы $\frac{7\pi}{10}$ $\frac{13\pi}{10}$
оба угла попадают в промежуток $[ \frac{\pi}{2} ; \frac{3\pi}{2} ]$ убывания. Так как это промежуток убывания, то если выполняется $x_2\ \textgreater \ x_1$ , то будет выполнятся $sin(x_1)\ \textgreater \ sin(x_2)$
у нас: $\frac{13\pi}{10} \ \textgreater \ \frac{7\pi}{10}$
и тогда $sin(\frac{13\pi}{10})\ \textless \ sin(\frac{7\pi}{10})$

Суть разобрали, и дальше легче.
Да и если углы из промежутка возрастания, то если $x_2\ \textgreater \ x_1$ , то выполняется $sin(x_2)\ \textgreater \ sin(x_1)$
---------------------------------------
углы 13п/7 и 11п/7 оба попадают в промежуток возрастания $[ \frac{3\pi}{2} ; \frac{5\pi}{2}]$
значит sin( 13п/7 ) > sin ( 11п/7 )
--------------------------------------------
оба угла -8п/7 и -9п/8 попадают в интервал убывания $[- \frac{3\pi}{2} ; -\frac{\pi}{2} ]$
-8п/7 < -9п/8, по этому<br>sin(-8п/7) > sin(-9п/8)
----------------------------------------------
оба угла 7 и 6 попадают в промежуток возрастания $[ \frac{3\pi}{2} ; \frac{5\pi}{2} ]$
7 > 6
sin(7) > sin(6)

90misha90_zn (30.4k баллов) 29 Апр, 18