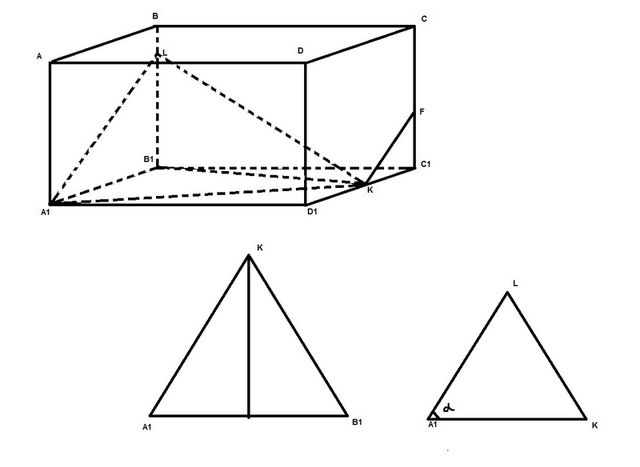
1) K - середина ребра C1D1. То есть D1K = KC1 = C1D1 / 2 = 12/2=6
2) B1L / LB = 4/1. Так как BB1 = 15, LB + 4*LB = 15, LB=3, B1L=4*LB=4*3=12
3) Проведем через K прямую, параллельную A1L. Она пересечет CC1 в точке F и будет частью плоскости (A1KL). Так как A1L || KF, 12/12 = 6 / C1F => C1F = 6.
Далее CF = CC1 - C1F = 15-6=9. Отвечаем на пункт а:
C1F / FC = 6/9 = 2/3.
4) Косинус угла между плоскостями (A1B1C1) и (A1KL) равен отношению площади проекции треугольника A1LK на плоскость (A1B1C1) то есть площади треугольника A1B1K к площади самого треугольника A1LK.
Сначала найдем площадь треугольника A1B1K. Высота, проведенная из вершины K, равна ребру A1D1 = 8. Основание, на которое падает высота, равно A1B1=12. Соответственно, площадь треугольника равна 1/2 * A1B1 * A1D1 = 1/2 * 12 * 8 = 48.
Теперь найдем площадь треугольника A1LK. Для этого найдем его стороны:
A1K: Из прямоугольного треугольника A1D1K найдем A1K = sqrt(A1D1^2 + D1K^2) = sqrt(8^2 + 6^2)=10.
A1L: Из прямоугольного треугольника A1B1L найдем A1L = sqrt(A1B1^2 + B1L^2) = sqrt(12^2 + 12^2) = 12*sqrt(2).
LK: Сначала из треугольника B1C1K найдем B1K = sqrt(B1C1^2 + C1K^2) = sqrt(8^2+6^2)=10. Затем из прямоугольного треугольника LB1K найдем уже LK = sqrt(B1L^2 + B1K^2) = sqrt(12^2 + 10^2)=sqrt(244) = 2*sqrt(61).
После того, как нашли все стороны треугольника A1LK, найдем косинус угла Найдем синус этого угла. sin 3/(5*sqrt(2)))^2) = sqrt(1 - 9/50) = sqrt(41)/(5*sqrt(2)).
Теперь можно найти площадь треугольника A1LK:
Она равна 1/2 * A1L * A1K * sin Отвечаем на вопрос б:
Косинус угла между плоскостями (A1LK) и (A1B1C1) равен 48 / (12*sqrt(41)) = 4/sqrt(41) = 4*sqrt(41)/41.