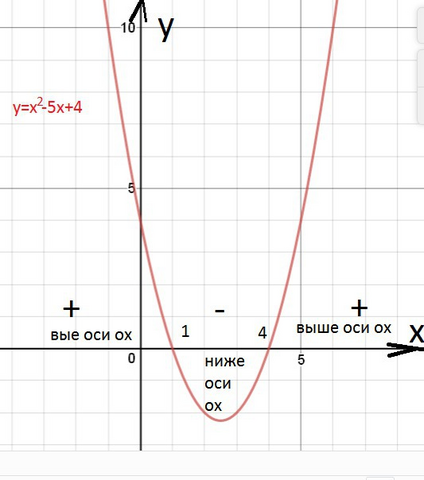
Метод интервалов основан на том, что график функции переходя из нижней полуплоскости в верхнюю или наоборот, пересекает ось ох в точке, которая называется нулем функции. И если график функции на отрезке (или интервале) расположен выше оси ох, это означает, что в любой точке этого отрезка(интервала) значение функции >0.
Поэтому выбираем любую точку. Находим значение функции только в ней и ставим такой же знак на всем интервале.
Найти нули функции, точки в которых
х²-5х+4=0
D=(-5)²-4·4=9
x=(5-3)/2=1 или х=(5+3)/2=4
Эти точки разбивают числовую прямую на три промежутка
________(1)_______(4)______
Находим знак на (4;+∞). Берем точку принадлежащую этому промежутку, например 10 и находим
10²-5·10+4=100-50+4>0
Ставим справа от точки 4 знак +
________(1)_______(4)___+___
Далее можем выбрать точки из (1;4). Например х=3
3²-5·3+4=9-15+4<0<br>Ставим знак -
________(1)___-____(4)___+___
и наконец, на (-∞;1) при х=0 получаем 4 >0
Ставим знак +
_____+___(1)___-___(4)___+___
Сравните знаки + - + на рисунке, на котором построен график функции. См. приложение.
О т в е т. (-∞;1) U(4;+∞)