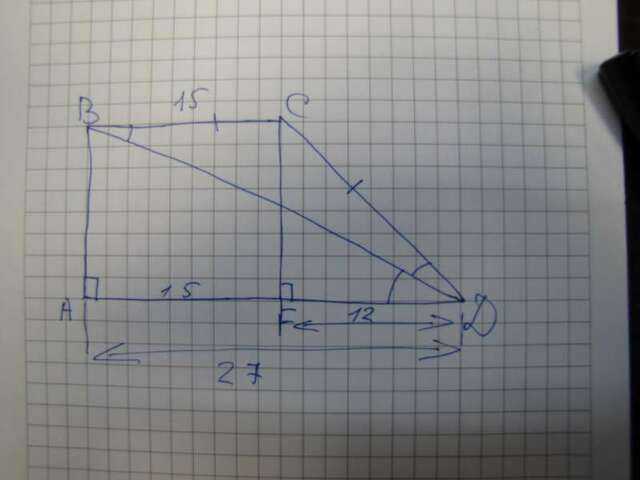
Прямоугольная трапеция ABCD c прямым углом A и основаниями BC=15 и AD=27 .∠CDB=∠BDA по условию .∠CBD=∠BDA как внутренние накрест лежащие при параллельных BC и AD и секущей BD .⇒∠CBD=∠CDB⇒ΔBCD- равнобедренный ⇒CD=BC=15 .Опустим высоту CF . ABCF-прямоугольник ⇒AF=BC=15⇒FD=AD-AF=27-15=12 .Треугольник CDF -прямоугольный ,по теореме Пифагора CF=√(CD²-FD²)=√(15²-12²)=9 .Площадь ABCD=((BC+AD)÷2)×CF=((15+27)÷2)×9=189 .