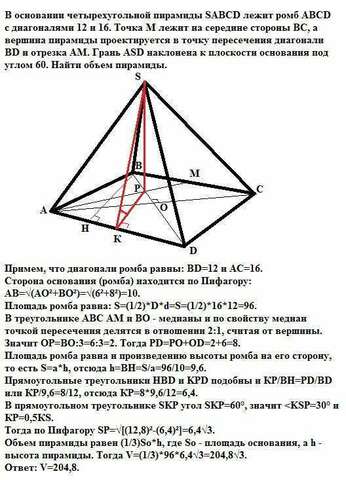
Примем, что диагонали ромба равны: ВD=12 и АС=16.
Сторона основания (ромба) находится по Пифагору:
АВ=√(АО²+ВО²)=√(6²+8²)=10.
Площадь ромба равна: S=(1/2)*D*d=S=(1/2)*16*12=96.
В треугольнике АВС АМ и ВО - медианы и по свойству медиан точкой пересечения делятся в отношении 2:1, считая от вершины.
Значит ОР=ВО:3=6:3=2. Тогда РD=PO+OD=2+6=8.
Площадь ромба равна и произведению высоты ромба на его сторону, то есть S=a*h, отсюда h=ВН=S/a=96/10=9,6.
Прямоугольные треугольники НВD и KPD подобны и КР/ВН=PD/BD или КР/9,6=8/12, отсюда КР=8*9,6/12=6,4.
В прямоугольном треугольнике SKP угол SKP=60°, значит Тогда по Пифагору SP=√[(12,8)²-(6,4)²]=6,4√3.
Объем пирамиды равен (1/3)So*h, где Sо - площадь основания, а h - высота пирамиды. Тогда V=(1/3)*96*6,4√3=204,8√3.
Ответ: V=204,8.