Помогите пожалуйста! Отдаю последние пункты. Отрезок АВ не пересекает плоскость альфа....

Question

73 просмотров

Помогите пожалуйста! Отдаю последние пункты.

Отрезок АВ не пересекает плоскость альфа. Расстояние от точки А до плоскости альфа равно 6 см, а от точки В до плоскости альфа 11 см. Найдите длину отрезка АВ, если его проекция на плоскость альфа равна 12 см.

Геометрия Maria1110_zn (12 баллов) 11 Март, 18 | 73 просмотров

Дан 1 ответ

Skifle_zn · Answer 1 · 2018-03-11T07:17:44+0000

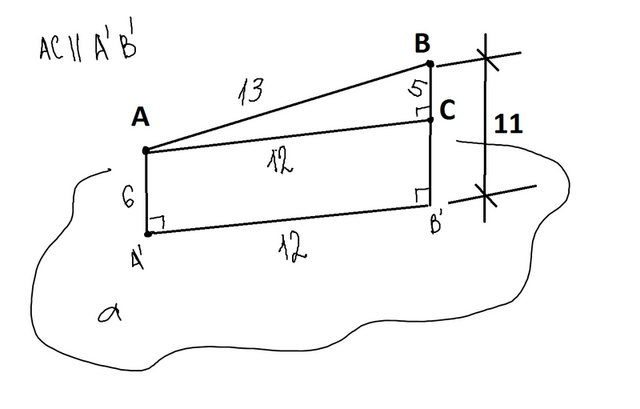
Проводим через точку А отрезок АС параллельный проекции А'В'

(AA'СB'-параллелограмм ,стороны AA'=СB' и AС=A'B')

получается прямоугольный треугольник сторона BC=BB' -СВ' 5=11-6(AA'=СB')

по теореме пифагора $AB^2=AC^2+BC^2$ $AB=\sqrt{12^2+5^2} =\sqrt{144+25}=\sqrt{169}=13$

между отрезками AA' и ВВ' и плоскостью прямой угол(90)

так как кратчайшее расстояние от точки до плоскости перепендикуляр