Вычислите плрщадь фигуры ограниченной линиями y=1-2x и y=3-2x-x^2

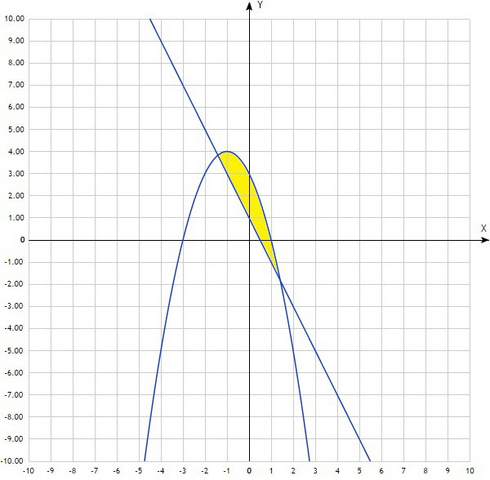
Прежде всего чертим чертёж. По нему определяем как выглядит фигура, площадь которой необходимо найти, какая функция больше на промежутке пересечения графиков функций и сам промежуток. Всё это необходимо для вычисления площади.
Итак, по рисунку видно, что график функции y=3-2x-x² лежит выше графика функции y=1-2x на промежутке [-√2;√2], значит функция y=3-2x-x², больше не этом промежутке. Точки пересечения графиков можно найти и аналитически, решив уравнение:
3-2x-x²=1-2x
-x²-2x+2x+3-1=0
-x²+2=0
x²=2
x=√2 x=-√2
Площадь фигуры, ограниченной линиями, находится по формуле
$s= \int\limits^b_a {(f(x)-g(x))} \, dx$
Подставляем значения функций и пределы интегрирования и находим площадь:
$s= \int\limits^{ \sqrt{2} }_{- \sqrt{2} } {(3-2x-x^2-1+2x)} \, dx = \int\limits^{ \sqrt{2} }_{- \sqrt{2} } {(2-x^2)} \, dx =2x- \frac{x^3}{3}|_{- \sqrt{2} }^{ \sqrt{2} }=$
$=2* \sqrt{2}- \frac{( \sqrt{2} )^3}{3}-(2*(- \sqrt{2)}- \frac{(- \sqrt{2} )^3}{3})= \frac{8 \sqrt{2} }{3}$ ≈3,77ед²