Можно решать методом интервалов.
Находим нули функции у=х²-7х+12.
х²-7х+12=0
D=(-7)²-4·12=49-48=1
x=(7-1)/2=3 или х=(7+1)/2=4
Эти точки разбивают числовую прямую на три промежутка
________[3]_____[4]__________
График любой функции переходя из верхней полуплоскости в нижнюю проходит через нуль ( точку пересечения с осью ох).
Поэтому если в какой-то точке интервала значение функции положительно, то оно положительно на всем интервале.
Находим знак в точке 10, например,
у(10)=10²-7·10+12 >0, значит на [4;+∞) функция принимает положительные значения, ставим +.
________[3]_____[4]____+______
Далее знаки чередуем.
___+____[3]__-__[4]____+______
О т в е т. x∈[3;4] или 3≤х≤4; это ответ под номером 1).
Можно решать графически.
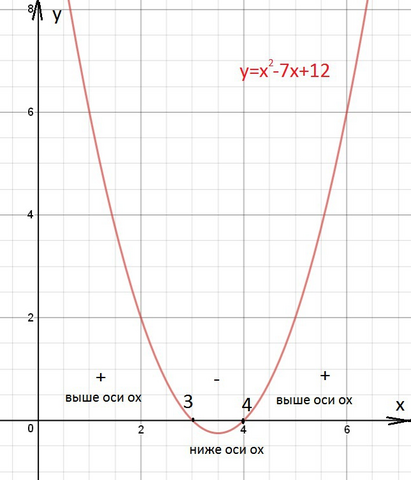
Графиком функции у=х²-7х+12 является парабола. Ветви параболы направлены вверх. См. рисунок в приложении
Парабола пересекает ось ох в двух точках
х=3 и х=4.
На (-∞;3] и на [4;+∞) парабола расположена выше оси Ох.
Значит выполняется неравенство
х²-7х+12 ≥0
На [3;4] парабола расположена ниже оси Ох.
Значит выполняется неравенство
х²-7х+12≤0
О т в е т. x∈[3;4] или 3≤х≤4; это ответ под номером 1).