Y'=(5x⁴-2x³+3x-7)'=20x³-6x²+3
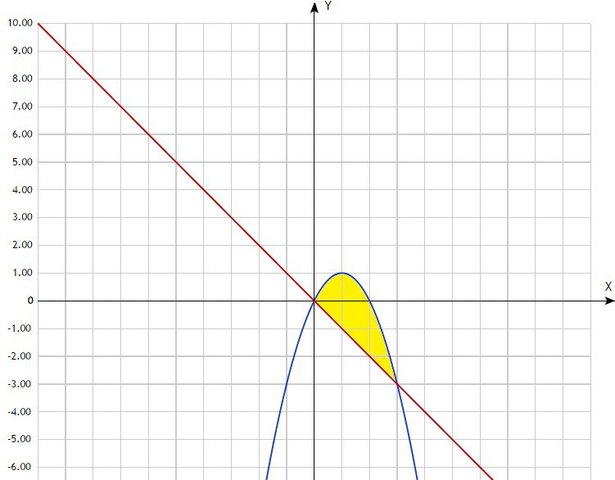
2) Чертим чертёж. Определяем пределы интегрирования, в наше случае это [0;3] (можно найти аналитически, решив уравнение:
2x-x²=-x
-x²+2x+x=0
3x-x²=0
x(3-x)=0
x=0 3-x=0
x=3
Далее по формуле площади, ограниченной линиями, вычисляем определённый интеграл
![S= \int\limits^3_0 {(2x-x^2-(-x))} \, dx= \int\limits^3_0 {(3x-[tex]=( \frac{3x^2}{2}- \frac{x^3}{3})|_0^3= \frac{3*3^2}{2}- \frac{3^3}{3}-0= \frac{3*3^3-2*3^3}{2*3}= \frac{3^3(3-2)}{2*3}= \frac{3^2}{2}=4,5](https://tex.z-dn.net/?f=S%3D+%5Cint%5Climits%5E3_0+%7B%282x-x%5E2-%28-x%29%29%7D+%5C%2C+dx%3D+%5Cint%5Climits%5E3_0+%7B%283x-%5Btex%5D%3D%28+%5Cfrac%7B3x%5E2%7D%7B2%7D-+%5Cfrac%7Bx%5E3%7D%7B3%7D%29%7C_0%5E3%3D+%5Cfrac%7B3%2A3%5E2%7D%7B2%7D-+%5Cfrac%7B3%5E3%7D%7B3%7D-0%3D+%5Cfrac%7B3%2A3%5E3-2%2A3%5E3%7D%7B2%2A3%7D%3D+%5Cfrac%7B3%5E3%283-2%29%7D%7B2%2A3%7D%3D+%5Cfrac%7B3%5E2%7D%7B2%7D%3D4%2C5++++++++ "S= \int\limits^3_0 {(2x-x^2-(-x))} \, dx= \int\limits^3_0 {(3x-[tex]=( \frac{3x^2}{2}- \frac{x^3}{3})|_0^3= \frac{3*3^2}{2}- \frac{3^3}{3}-0= \frac{3*3^3-2*3^3}{2*3}= \frac{3^3(3-2)}{2*3}= \frac{3^2}{2}=4,5")
x^2)} \, dx= [/tex] ед².
