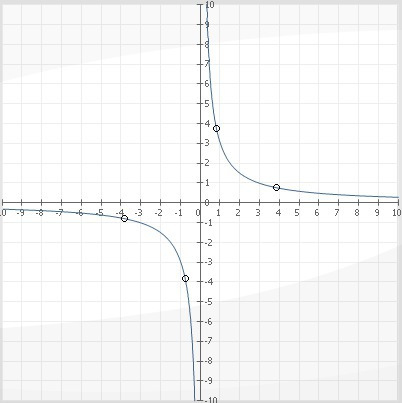
(xy-3)/(x^2+y^2-16)=0 эквивалентно xy=3, x^2+y^2-16≠0.
xy=3 - гипербола
x^2+y^2=16 - окружность радиуса 4.
График (xy-3)/(x^2+y^2-16)=0 представляет собой множество точек xy=3 c выколотыми точками, которые принадлежат и x^2+y^2=16.
Найдем точки пересечения xy=3 и x^2+y^2=16.
y=3/x. Поставим это во второе уравнение.
x^2+(3/x)^2=16
x^4 - 16x^2 + 9 = 0
Пусть x^2=t. Тогда перейдем к квадратному уравнению t^2-16t+9=0
D=(-16)^2-4*9=220
t1,2=(16+-√220)/2=8+-√55
Оба корня больше 0. Поэтому уравнение имеет 4 решения для x:
x1,2,3,4=+-√(8+-√55)
Им соответствуют корни для y (подставляем в уравнение y=3/x):
y1,2,3,4=+-√(8-+√55).