Різниця відстаней від точки кола до кінців діаметра дорівнює 10 см,а радіус кола-25...

Question

Різниця відстаней від точки кола до кінців діаметра дорівнює 10 см,а радіус кола-25 см.Обчисліть відстань від цієї точки до діаметра

Answer 1

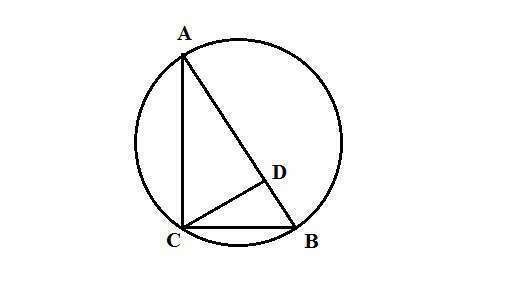
Дивись малюнок. Діаметр АВ = 50 см. Точка на колі - С. Відстані від точки С до кінців діаметра АС і ВС. Так як кут АСВ спирається на діаметр, то він прямий.
Нехай ВС=х см, тоді АС=х+10 см.  За т. Піфагора:
х²+(х+10)²=50²
х²+х²+20х+100-2500=0
2х²+20х-2400=0
х²+10х+1200=0
Д=100+4800=4900
х1=-80/2=-40 (від"ємне значення не приймаємо)
х2=60/2=30 см
х+10=30+10=40 см
АС=40 см, ВС=30 см.

Нехай АД=а см. Виразимо СД з двох прямокутних трикутників СДВ та СДА за т. Піфагора:
СД²=40²-а²
СД²=30²-(50-а)²
40²-а²=30²-(50-а)²
1600-а²=900-2500+100а-а²
100а=3200
а=32 см
СД²=40²-32²=576
СД=24 см

---

Answer 2

∠ABC = 90° (опирается на диаметр)
AC = 2R
AC = 2 · 25 = 50 см

Пусть AB = x см, тогда BC = x + 10 см.
Составим теорему Пифагора для ΔABC
 x² + (x + 10)² = 50²
x² + x² + 20x + 100 = 2500
2x² + 20x - 2400 = 0
x² + 10x - 1200 = 0
D = 5² + 4 · 1200 = 4900 = 70²
x₁ = (-10 + 70) / 2 = 30
x₂ = (-10 - 70) / 2 = -40 - не уд.

Значит AB = 30 см
BC = 30 + 10 = 40 см

SΔABC = ½ AB · BC = ½ AC · BH
AB · BC = AC · BH
BH = AB · BC / AC
BH = 30 см · 40 см / (50 см) = 24 см

Ответ: 24 см

---