Помогите пожалуйста!!!

Question

Дан 1 ответ

laymlaym2_zn · Answer 1 · 2018-03-11T07:45:57+0000

A1. $\sqrt[4]{a}:a^{-\frac{1}{2}}=\frac{\sqrt[4]{a}}{a^{\frac{1}{2}}}=\frac{\sqrt[4]{a}}{\sqrt{a}}=\frac{\sqrt[4]{a}}{\sqrt[4]{a^2}}=\sqrt[4]{\frac{a}{a^2}}=\sqrt[4]{\frac{1}{a}}=\frac{1}{\sqrt[4]{a}}$

A2. $\frac{b^\frac{2}{5}-25}{b^\frac{1}{5}+5}-b^\frac{1}{5}=\frac{(b^\frac{1}{5})^2-5^2}{b^\frac{1}{5}+5}-b^\frac{1}{5}=\frac{(b^\frac{1}{5}-5)(b^\frac{1}{5}+5)}{b^\frac{1}{5}+5}-b^\frac{1}{5}=b^\frac{1}{5}-5-b^\frac{1}{5}=\\=-5$

A3. $log_318-log_32+5^{log_52}=log_3\frac{18}{2}+2=log_39+2=2+2=4$

A4.\frac{1}{8}\\(\frac{1}{2})^{x-2}>(\frac{1}{2})^3\\x-2<3\\x<5" alt="(\frac{1}{2})^{x-2}>\frac{1}{8}\\(\frac{1}{2})^{x-2}>(\frac{1}{2})^3\\x-2<3\\x<5" align="absmiddle" class="latex-formula">

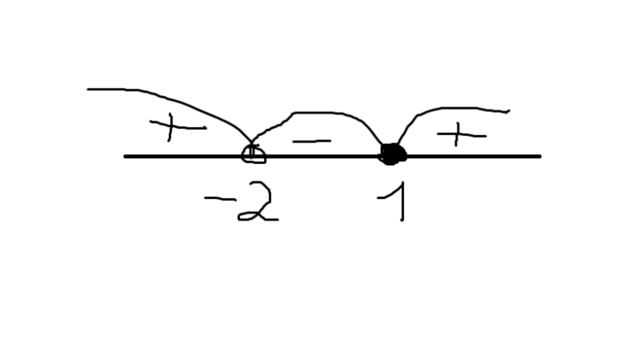
A5. [-3;0]

A6. $2cos^2\frac{\alpha}{2}-cos\alpha-1=1+cos\alpha-cos\alpha-1=0$

A7. $log_2x=\frac{1}{2}\\x=2^\frac{1}{2}\\x=\sqrt{2}$

A8. $log_2(x-2)=3\\x-2=2^3\\x=8+2\\x=10$

A9. $\frac{x-1}{x+2}\geq0\\f(x)=\frac{x-1}{x+2}\\D(f):x+2\neq0\ \ \ \ \ \ \ \ x\neq-2\\f(x)=0\\x-1=0\\x=1$

Рисуем интервал наносим на его точки. Вложение. х принадлежит: $(-\infty;-2)\cup[1;+\infty)$

A10. $9^x\leq\frac{1}{3}\\3^{2x}\leq3^{-1}\\2x\leq-1\\x\leq-\frac{1}{2}$

A11.20\\2^x(2^{x+2-x}+2^{x-x})>20\\2^x(4+1)>20\\2^x>4\\2^x>2^2\\x>2" alt="2^{x+2}+2^x>20\\2^x(2^{x+2-x}+2^{x-x})>20\\2^x(4+1)>20\\2^x>4\\2^x>2^2\\x>2" align="absmiddle" class="latex-formula">

A12. $lg^2x-3lgx-10=0\\lgx=t\\t^2-3t-10=0\\D=9+40=49\\x_{1}=\frac{3+7}{2}=5\\x_{2}=\frac{3-7}{2}=-2\\lgx=5\ \ \ \ \ \ \ \ lgx=-2\\x=10^5\ \ \ \ \ \ \ \ x=10^{-2}\\10^5*10^{-2}=10^{5-2}=10^3=1000$

A13. $2cos^2x-3sinx=0\\2(1-sin^2x)-3sinx=0\\2-2sin^2x-3sinx=0\\2sin^2x+3sinx-2=0\\sinx=t;-1\leq t\leq1\\2t^2+3t-2=0\\D=9+16=25\\x_{1}=\frac{-3+5}{4}=-\frac{1}{2}\ \ \ \ \ \ x_{2}=\frac{-3-5}{4}=-2$

x2 неудовлетворяет условию.

$sinx=-\frac{1}{2}\\x=(-1)^{m+1}*arcsin(\frac{1}{2})+\pi*m\\x=(-1)^{m+1}*\frac{\pi}{6}+\pi*m$

m принадлежит Z.

В1.0\\t^2-6t+8=0\\D=36-32=4\\x_{1}=\frac{6+2}{2}=4\\x_{2}=\frac{6-2}{2}=2\\2^x=4\ \ \ \ \ \ \ \ 2^x=2\\2^x=2^2\ \ \ \ \ \ \ 2^x=2^1\\x=2\ \ \ \ \ \ \ \ \ \ x=1\\1*2=2" alt="\frac{1}{6*2^x-11}=\frac{1}{4^x-3}\ \ \ \ \ \ \ \ \ \ |*(6*2^x-11)(4^x-3)\neq0\\\frac{(6*2^x-11)(4^x-3)}{6*2^x-11}=\frac{(6*2^x-11)(4^x-3)}{4^x-3}\\4^x-3=6*2^x-11\\2^{2x}-6*2^x+8=0\\2^x=t,t>0\\t^2-6t+8=0\\D=36-32=4\\x_{1}=\frac{6+2}{2}=4\\x_{2}=\frac{6-2}{2}=2\\2^x=4\ \ \ \ \ \ \ \ 2^x=2\\2^x=2^2\ \ \ \ \ \ \ 2^x=2^1\\x=2\ \ \ \ \ \ \ \ \ \ x=1\\1*2=2" align="absmiddle" class="latex-formula">

B2. Почемуто неполучилось. Промежуток у меня x>21/9

B3. $(\sqrt[6]{7}-\sqrt[6]{2})(\sqrt[6]{7}-\sqrt[6]{2})((\sqrt[3]{7}+\sqrt[3]{2})^2-\sqrt[3]{14})=\\=(\sqrt[6]{7^2}-\sqrt[6]{2^2})(\sqrt[3]{7^2}+2\sqrt[3]{7*2}+\sqrt[3]{2^2}-\sqrt[3]{14})=\\=(\sqrt[3]{7}-\sqrt[3]{2})(\sqrt[3]{7^2}+\sqrt[3]{14}+\sqrt[3]{2^2})=\\=\sqrt[3]{7^2*7}+\sqrt[3]{14*7}+\sqrt[3]{2^2*7}-\sqrt[3]{7^2*2}-\sqrt[3]{14*2}-\sqrt[3]{2^2*2}=\\=7+\sqrt[3]{98}+\sqrt[3]{28}-\sqrt[3]{98}-\sqrt[3]{28}-2=5$