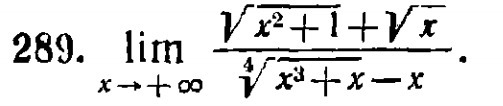Очень прошу решить этот пример: тема лимиты, решала разными способами, но ответы получаются разные. Проверила на wolframalpha, ответ -1, а как решить не знаю. Помогите пожалуйста!
Если что - это задачник Бермана "Сборник задач по курсу мат. анализа", номер 289)